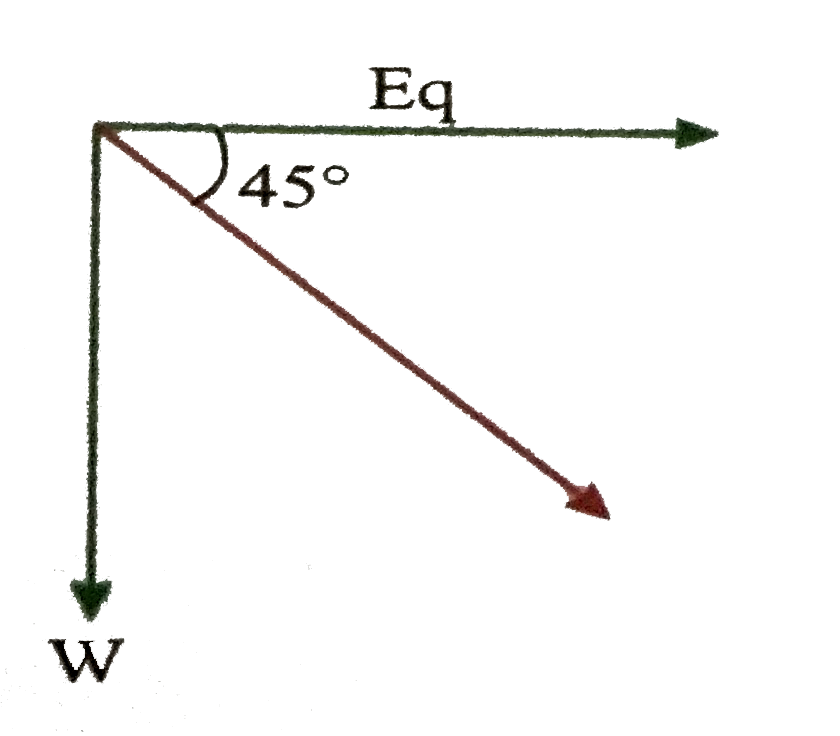
In the Millikan's experiment, the oil drop is subjected to a horizontal electric field of 2 N//S and the drop moves with a constant velocity making an angle of 450with the horizontal . If the weight of the drop is W, then the electric charge, in coulomb, on the drop is
W
W/2
W/4
w/8
The correct Answer is:B
Tan450=Eqw Eq=w
Topper's Solved these Questions
Similar Questions
A man walks in rain with a velocity of 5 kmph. The rain drops strike at him at an angle of 45∘ with the horizontal. The downward velocity of the rain drops will be :
View SolutionIn the Millikan's experiment, the distance between two horizontal plates is 2.5 cm and the potential difference applied is 250 V .The electric field between the plates will be
View Solution
Knowledge Check
- Question 1 - Select One
In the Millikan’s Oil Drop experiment, the oil drop is subjected to such forces whose nature does NOT fall under the category of:
AelectrostaticBgravitationalCviscousDmagnetostatic - Question 2 - Select One
In the Millikan’s Oil Drop experiment, the oil drop is subjected to such forces whose nature does NOT fall under the category of:
AA)electrostaticBB)viscousCC)gravitationalDD) magnetostatic - Question 3 - Select One
In Millikan's oil drop experiment, we make use of:
AOhm's lawBAmpere's lawCStoke's lawDFaraday's law
In Millikan's oil drop experiment, an oil drop mass 60×10−6kg is balanced by an electric field of 106V/m. The charge in coulomb on the drop, assuming g=10m/s2 is
View SolutionA: The oil-drops of Millikan's experiment should be microscopic size.
R: For larger drops the electric fields needed in the experiment will be impractically high.View SolutionIn Millikan's oil drop of mass 16×10−6kg is balanced by an electric field of 106V/m. The charge in coulomb on the drop is: (assuming g=10m/s2)
View SolutionIn Millikan's oil drop of mass 16×10−6kg is balanced by an electric field of 106V/m. The charge in coulomb on the drop is: (assuming g=10m/s2)
View SolutionIn a Millikan's oil drop experiment the charge on an oil drop is calculated to be 16.35×10−19C. The number of excess electrons on the drop is
View Solution

