The number of molecules per unit volume (n) of a gas is given by
PkT
kTP
PkT
RTP
The correct Answer is:A
To find the number of molecules per unit volume (n) of a gas, we can use the ideal gas law and some fundamental constants. Here’s a step-by-step solution:
1. Start with the Ideal Gas Law:
The ideal gas law is given by the equation:
PV=nRT
where:
- P = pressure of the gas
- V = volume of the gas
- n = number of moles of the gas
- R = universal gas constant
- T = absolute temperature of the gas
2. Rearrange the Ideal Gas Law:
To find the number of moles per unit volume, we can rearrange the equation:
n=PVRT
3. Convert Moles to Molecules:
The number of molecules N can be expressed in terms of moles using Avogadro's number NA:
N=n×NA
Substituting the expression for n from the previous step:
N=(PVRT)×NA
4. Express Volume per Unit Volume:
Since we are interested in the number of molecules per unit volume, we can express the volume V as 1 (for unit volume):
N=P×1RT×NA=PRT×NA
5. Using Boltzmann's Constant:
We know that the universal gas constant R can be expressed in terms of Boltzmann's constant k:
R=NA×k
Substituting this into our equation gives:
N=PkT
6. Final Result:
Therefore, the number of molecules per unit volume n is given by:
n=PkT
Final Answer:
The number of molecules per unit volume n of a gas is:
n=PkT
The ideal gas law is given by the equation:
PV=nRT
where:
- P = pressure of the gas
- V = volume of the gas
- n = number of moles of the gas
- R = universal gas constant
- T = absolute temperature of the gas
To find the number of moles per unit volume, we can rearrange the equation:
n=PVRT
The number of molecules N can be expressed in terms of moles using Avogadro's number NA:
N=n×NA
Substituting the expression for n from the previous step:
N=(PVRT)×NA
Since we are interested in the number of molecules per unit volume, we can express the volume V as 1 (for unit volume):
N=P×1RT×NA=PRT×NA
We know that the universal gas constant R can be expressed in terms of Boltzmann's constant k:
R=NA×k
Substituting this into our equation gives:
N=PkT
Therefore, the number of molecules per unit volume n is given by:
n=PkT
The number of molecules per unit volume n of a gas is:
n=PkT
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-I(C.W)32videos
KINETIC THEORY OF GASES
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-II(C.W)25videos
KINETIC THEORY OF GASES
- BOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - SOLVED EXAMPLE83videos
KINETIC THEORY OF GASES
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EXERCISE -IV40videos
GRAVITATION
- BOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - IV35videos
LAW OF MOTION
Similar Questions
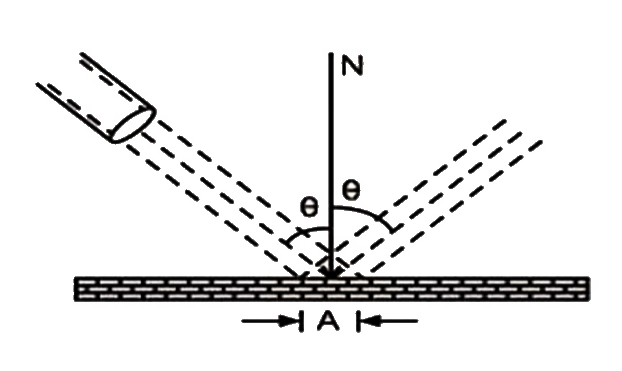
A nozzle throws a stream of gas against a wall with a velocity v much larger than the thermal agitation of the molecules. After collision of the molecules with wall the magnitude of their velocity remains same. Also assume that the force exerted on the wall by the molecule is perpendicular to wall. (This is not strictly true for a rough wall.) Find the pressure exerted on the wall. (n = number of molecules per unit volume, m = mass of a gas molecule)
 View Solution
View SolutionFind the number of molecules per unit volume of oxygen at NTP. [Mass of an oxygen molecule = 5.313×10−26 kg, rms speed of oxygen molecles at NTP = 461.2 m/s]
View Solution
Knowledge Check
- Question 1 - Select One
If P=106kT, then the number of molecules per unit volume of the gas is [the letters have usual meanings.]
A100KB300KC502KD546K - Question 2 - Select One
KE per unit volume is:
A32PB32RTC32RNN0D32RTn - Question 3 - Select One
Kinetic energy per unit volume of a gas is
A3P2B2P3CP2DP3
If P is the pressure,V the volume,R the gas constant,k the Boltzmann constant and T the absolute temperature,then number of molecules in the given mass of the gas is given
View SolutionThe molar gas volume at S.T.P is 22.4 litre and Avogadro's number is 6.023×1023. Calculate (i) number of gas molecules per unit volume (ii) radius of gas molecule when mean free path is 1.1×10−8m.
View SolutionNumber of particles is given by n=−Dn2−n1x2−x1 crossing a unit area perpendicular to X-axis in unit time, where n1 and n2 are number of particles per unit volume for the value of x meant to x2 and x1. Find dimensions of D called as diffusion constant
View SolutionWhich of the following represents the mean free path for a gas ? (where n is number of gas molecules per unit volume, d is diameter of gas molecules)
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
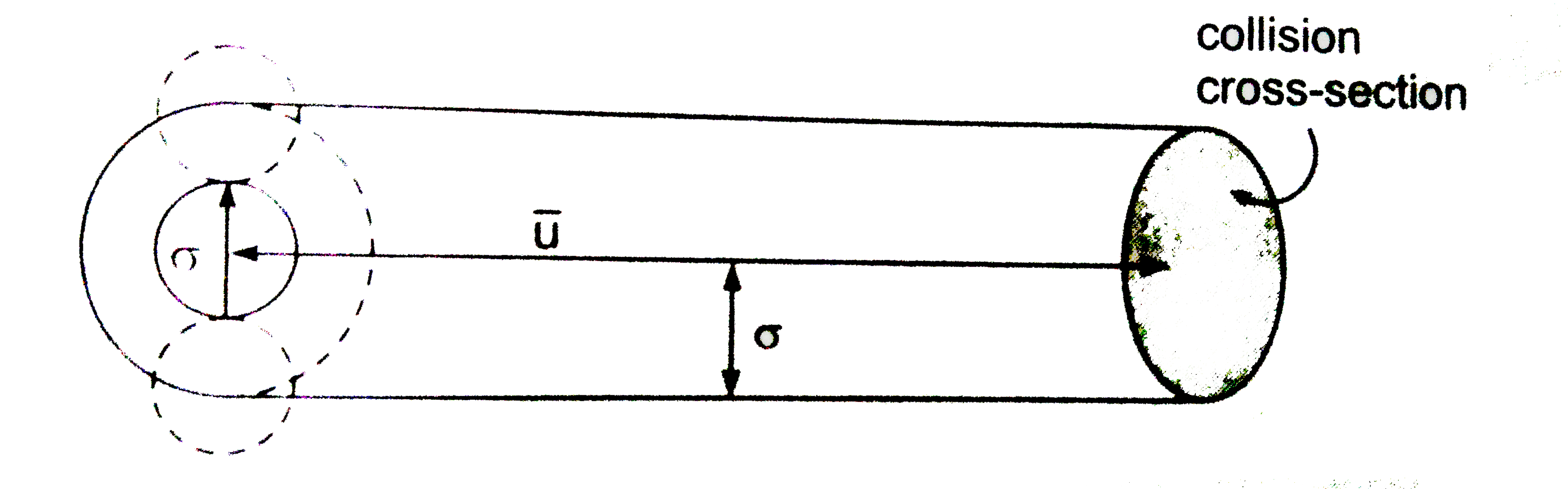
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
Three ideal gas samples in separate equal volume containers are taken and following data is given :
PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate ratio of collision frequencies (Z11)(A:B:C) of following for the three gases.View Solution

