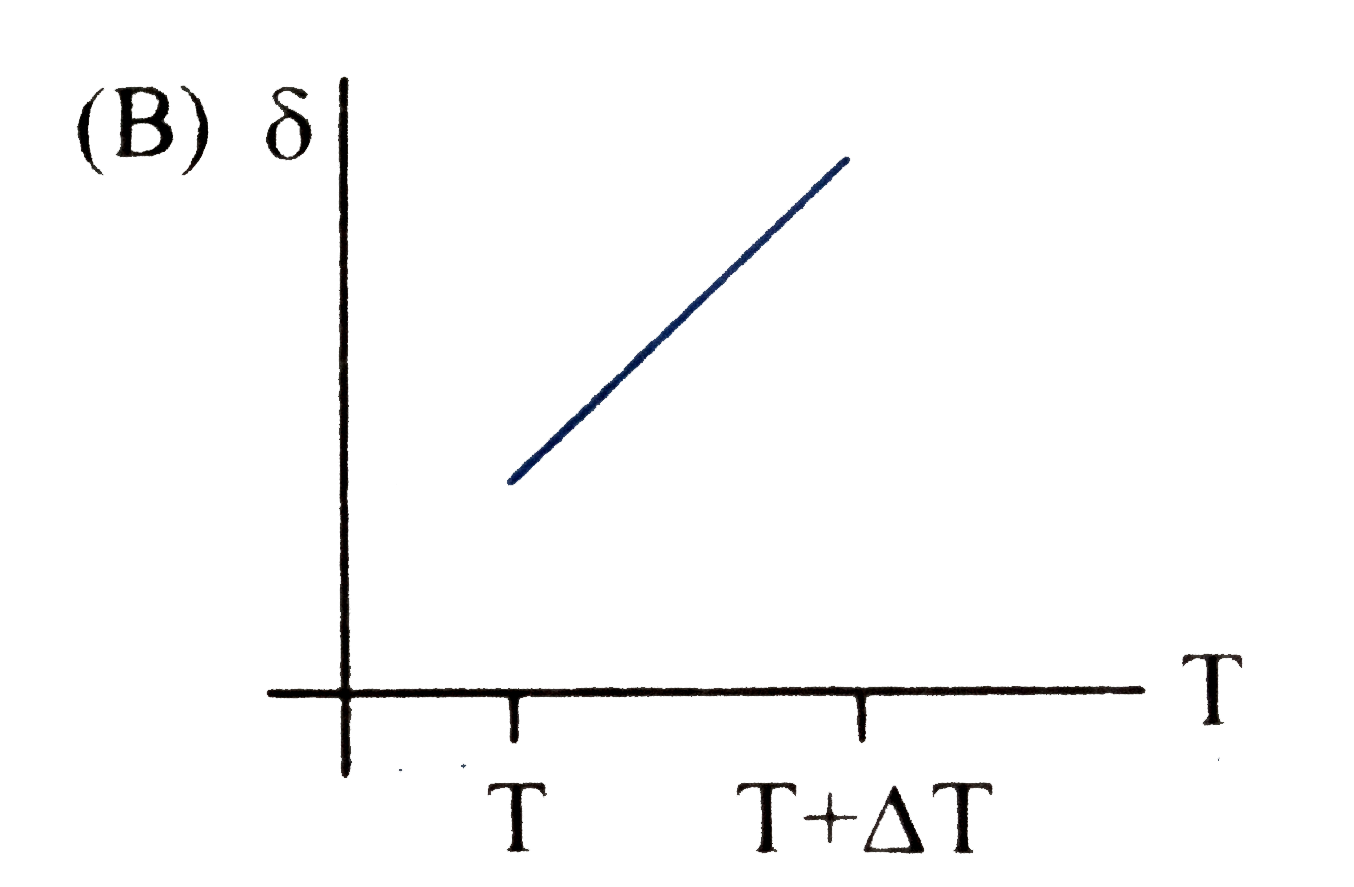
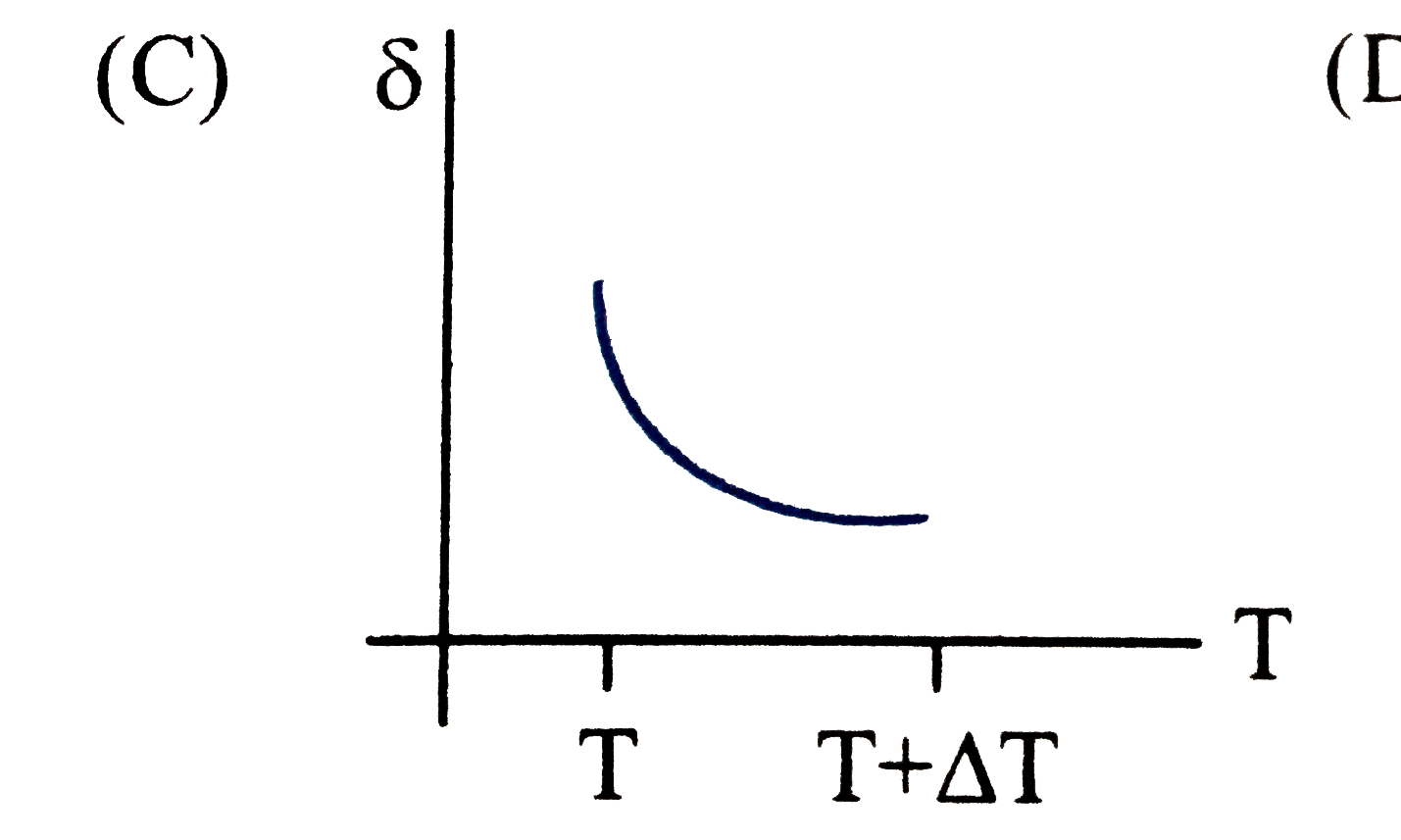
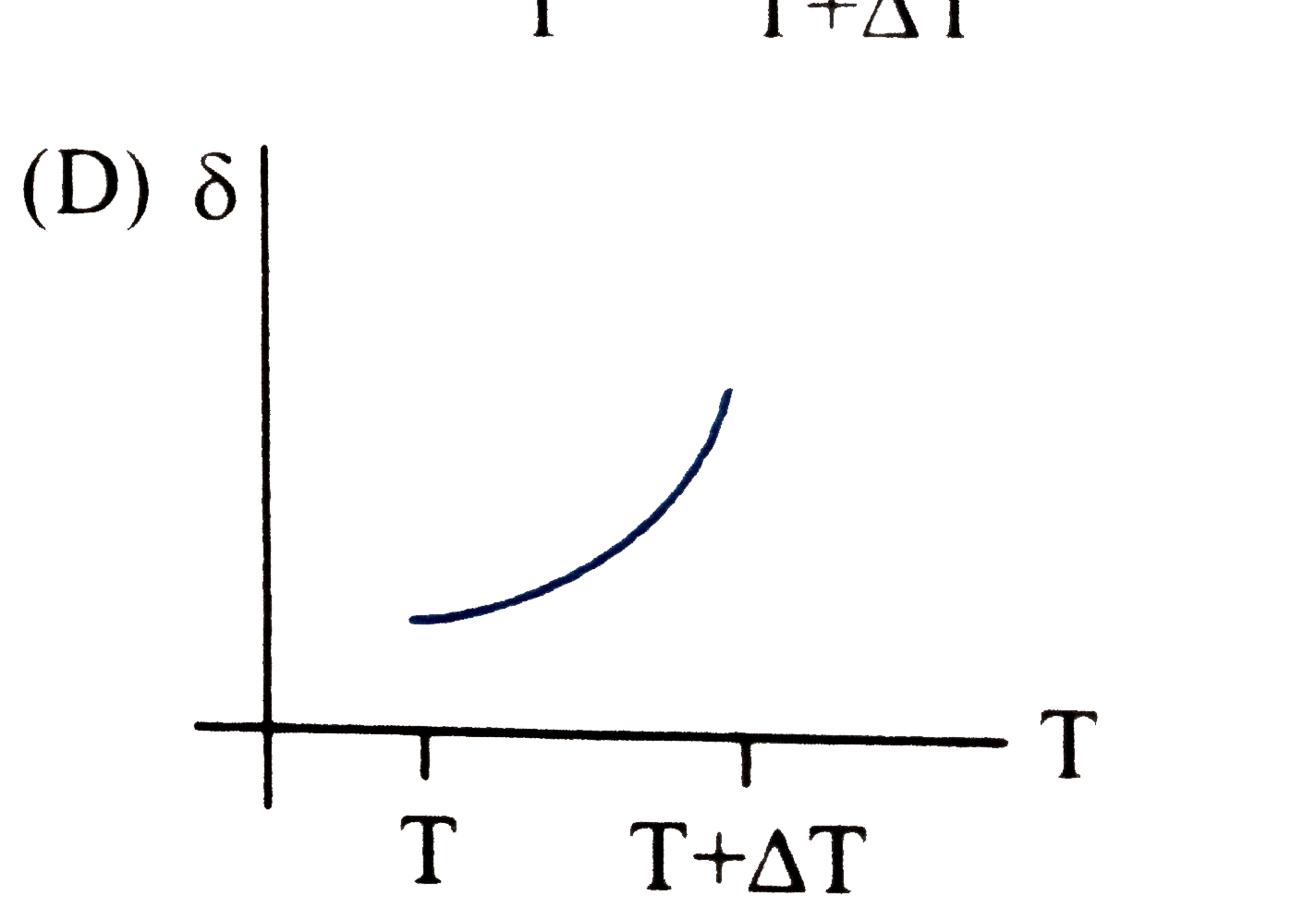
An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
A

B
C
D
Video Solution
Text Solution
The correct Answer is:C
For a given mass of gas at constant pressure.
VT= constant ∴V+ΔVT+ΔT=VT
or VT+VΔT=VT+TΔV or VΔT=TΔV
or 1T=ΔVVΔT or 1T=δ or δT=1
The equation represents a rectangular hyperbola of the form xy=c2.
Hence the δ−T variation is represented by graph (c).
|
Topper's Solved these Questions
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-VI
10 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-I (H.W)
12 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - NCERT BASED QUESTIONS
28 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EXERCISE -IV
40 Videos
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - IV
35 Videos
Similar Questions
Knowledge Check
An ideal gas is initially at temperature T and volume V. It's volume increases by ΔV due to an increase in temperature of ΔT, pressure remaining constant. The quantity μ=ΔVVΔT varies with temperature as -
A B
B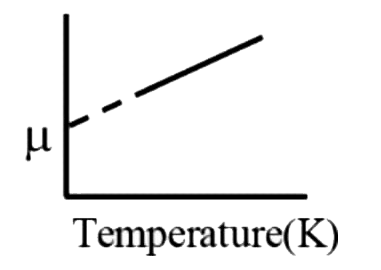 C
C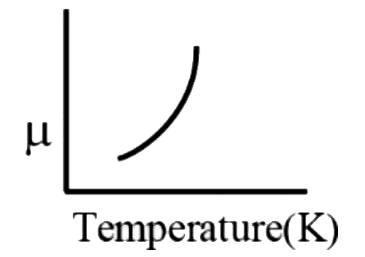 D
D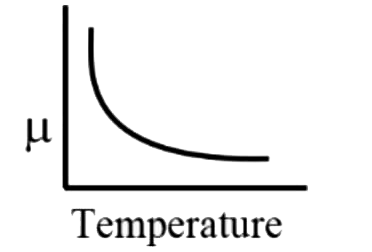
An ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
A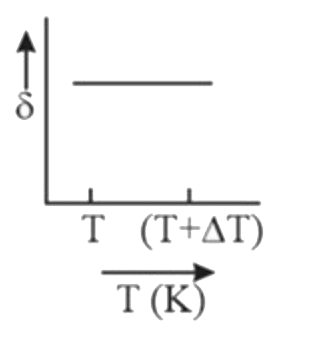 B
B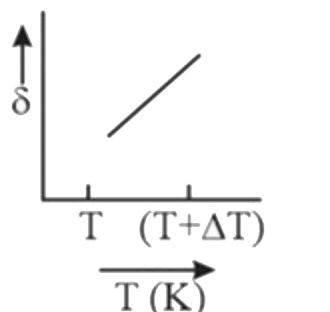 C
C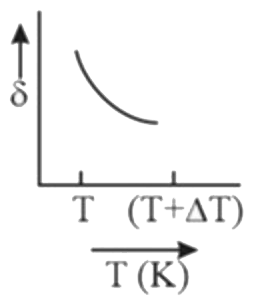 D
D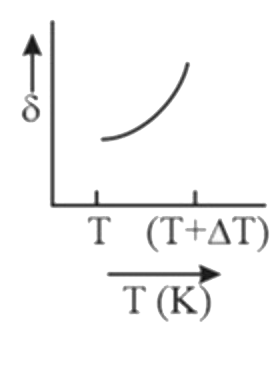
A constant temperature , the volume of a gas is to be decreased by 4 % The pressure must be increased by
A0.04B0.0416C0.08D0.0386
At constant volume, temperature is increased. Then
View SolutionThe volume of a gas is increasing adiabatically. Its temperature
View SolutionBy increasing temperature of a gas by 6∘C its pressure increases by 0.4%, at constant volume. Then initial temperature of gas is
View SolutionBy increasing temperature and keeping the volume constant, the pressure of a gas will
View SolutionBy increasing temperature and keeping the volume constant, the pressure of a gas will
View Solution
