A very small circular loop of radius r is initially coplanar and concentric with a much larger circular loop of radius R(>>r) . A constant current i is passed in the larger loop which is kept fixed in space and the small loop is rotated with angular velocity ω about a diameter. The resistance of the small loop is R0 and the inductance is negligible.
(a) Find the current in the small loop as a function of time.
(b) Calculate how much troque must be exerted on the small loop to rotate it.
Magnetic field due to large loop at centre
B=μ0i2R⊗
Let at any time t , normal to small loop makes angle θ(=ωt) with magnetic field
(a) Flux throuth smaller loop
ϕ=Bacosthe
=μ0i2R.πr2cosωt
e=−dϕdt=μ0iπr2ωsinωt2R
Induced current
I=eR0=μ0iπr2ωsinωt2R0
(b) Torque on smaller loop
τ=MBsinθ
=Iπr2Bsinωt
=μ0iπr2ω.πr22R0.μ0i2Rsin2ωt
=μ20i2π2r2ω4R2R0sin2ωt

Related Playlists
Similar Practice Problems
- Question 1 - Select One
A very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b (>>a). A constant current is passed in the large loop which is kept fixed in space & the small loop is rotated with angular velocity omega about a diameter. The resistance of the small loop is R & its self inductance is negligible. The current in the larger loop is clockwise.
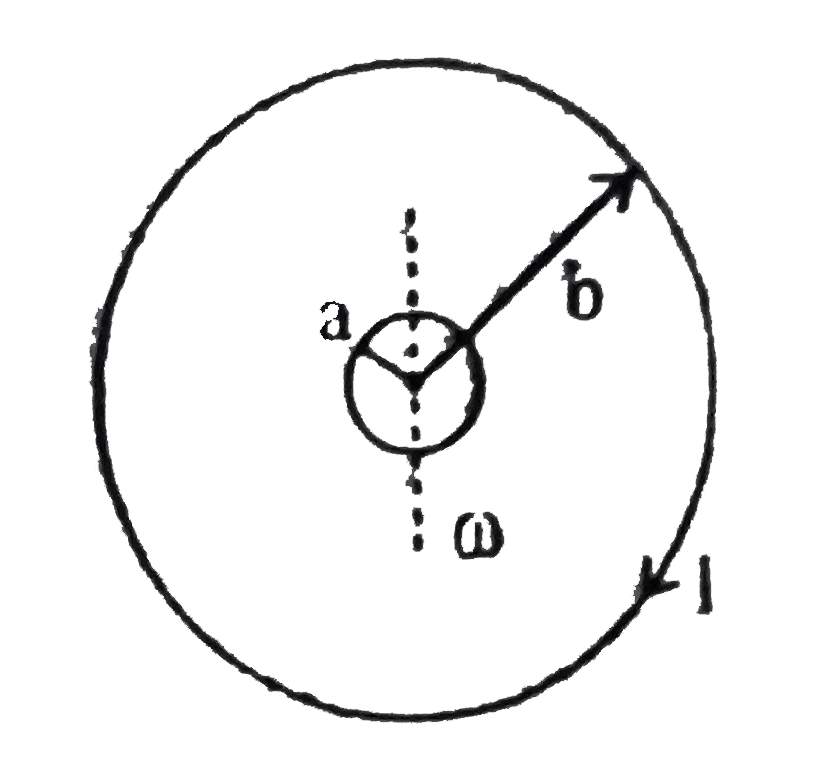
Find the current in the small loop as a function of time.Aπa2μ0Iωsinωt2bRBπa2μ0Iωcosωt2bRCπb2μ0Iωsinωt2aRDπb2μ0Iωcosωt2aR - Question 1 - Select One
A very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b (>>a). A constant current is passed in the large loop which is kept fixed in space & the small loop is rotated with angular velocity omega about a diameter. The resistance of the small loop is R & its self inductance is negligible. The current in the larger loop is clockwise.
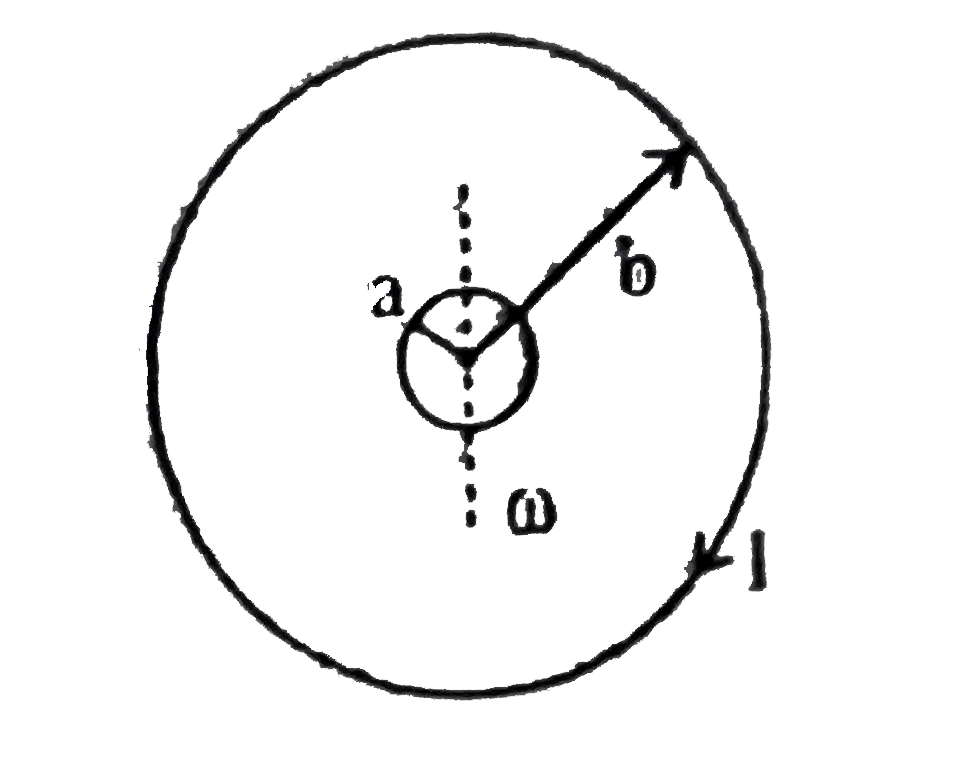
Calculate how much torque must be exerted on the small loop to rotate it.AωR(πb2μ0Isinωt2b)2BωR(πb2μ0I2b)2sinωtcosωtCωR(πa2μ0Isinωt2b)2DNone of these - Question 1 - Select One
A very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b (>>a). A constant current is passed in the large loop which is kept fixed in space & the small loop is rotated with angular velocity omega about a diameter. The resistance of the small loop is R & its self inductance is negligible. The current in the larger loop is clockwise.
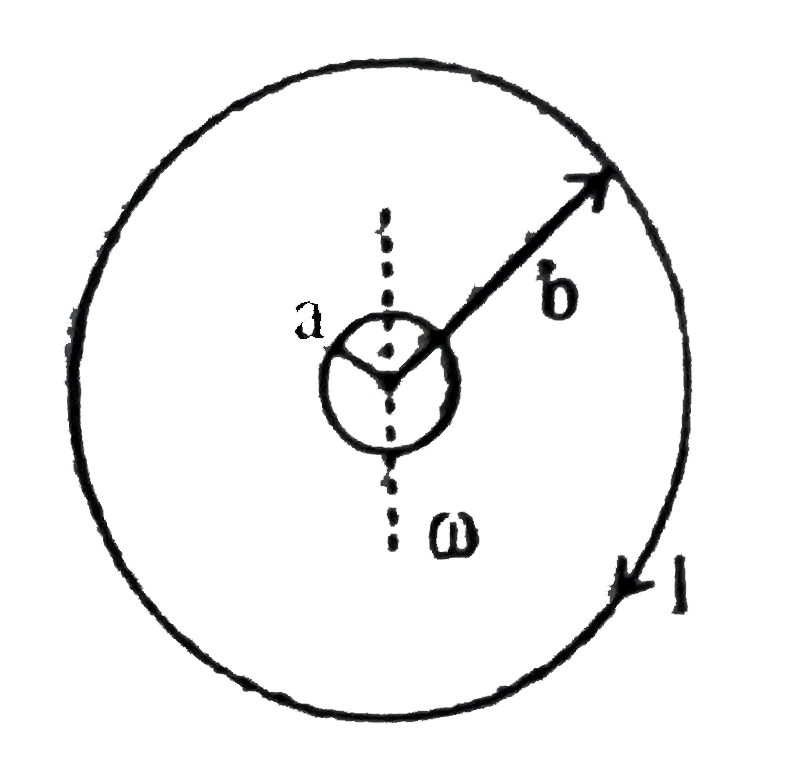
At the moment both the loops are in the same planeAthe induced current in small loop is zero.Bthe induced current in small loop is clockwise.Cthe induced current in small loop is in anticlockwise direction.Dthe induced current is clockwise or anticlockwise depending on sense of angular velocity vector. - Question 1 - Select One
A very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is
Aπa2μ0I2bωcos(ωt)Bπa2μ0I2bωsin(ω2t2)Cπa2μ0I2bωsin(ωt)Dπa2μ0I2bωsin2(ωt) - Question 1 - Select One
A very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is
Aπa2μ0I2bωcosωtBπa2μ0I2bωsinω2t2Cπa2μ0I2bωsinωtDπa2μ0I2bωsin2ωt - Question 1 - Select One or More
A uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
 A(a) zero, when θ is zeroB(b) πa2Bω2R, when θ is zeroC( c) zero, when θ=π/2D(d) πa2Bω2R, when θ=π/2
A(a) zero, when θ is zeroB(b) πa2Bω2R, when θ is zeroC( c) zero, when θ=π/2D(d) πa2Bω2R, when θ=π/2 - Question 1 - Select One
The linear loop has an area of 5×10−4m2 and a resistance of 2Ω. The larger circular loop is fixed and has a radius of 0.1m. Both the loops are concentric and co-planner. The smaller loop is rotated with an angular velocity ωrads−1 about its dismeter. The magnetic flux with the smaller loop is
 A2π×10−6WbBπ×x10−9WbCπ×10−9cosωtWbDzero
A2π×10−6WbBπ×x10−9WbCπ×10−9cosωtWbDzero
Similar Questions
A very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b(<<a).A constant current I is passed in the large loop which is kept fixed in space & the small loop is rotated with constant angular velocity ω about a diameter.The resistance of the small loop is R & its inductance is negligible The induced emf in the large loop due to current induced in smaller loop as a function of time is equal to 1x(πa2μ0ωb)2Icos2ωtR.Find out value of x.
View SolutionA very small circular loop of area 5×I0−4m2 , resistance 2Ω and negligible inductance is initially coplanar and concentric with a much larger fixed circular loop of radius 0.Im . A constant current of IA is passed in the bigger loop and the smaller loop is rotated with angular velocity ωrad/sec about a diameter. Calculate (a) the flux limked with the smaller loop, (b) indced emf (c) induced current in the smaller loop, as a function of time.
View SolutionA small circular loop of radius a is placed inside a large square loop of edge L(>>a) . The loops are coplanar and concentric. Find mutual inductance.
View Solution

