A converging lens forms a real image I on its optic axis. A rectangular galss slab of refractive index μ and thickness t is introduced between the lens and I. I will move
away from the lens by (μ−1)
towards the lens by t(μ−1)
away from the lens by t(μ−1μ)
towards the lens by t(μ−1μ)
The correct Answer is:C
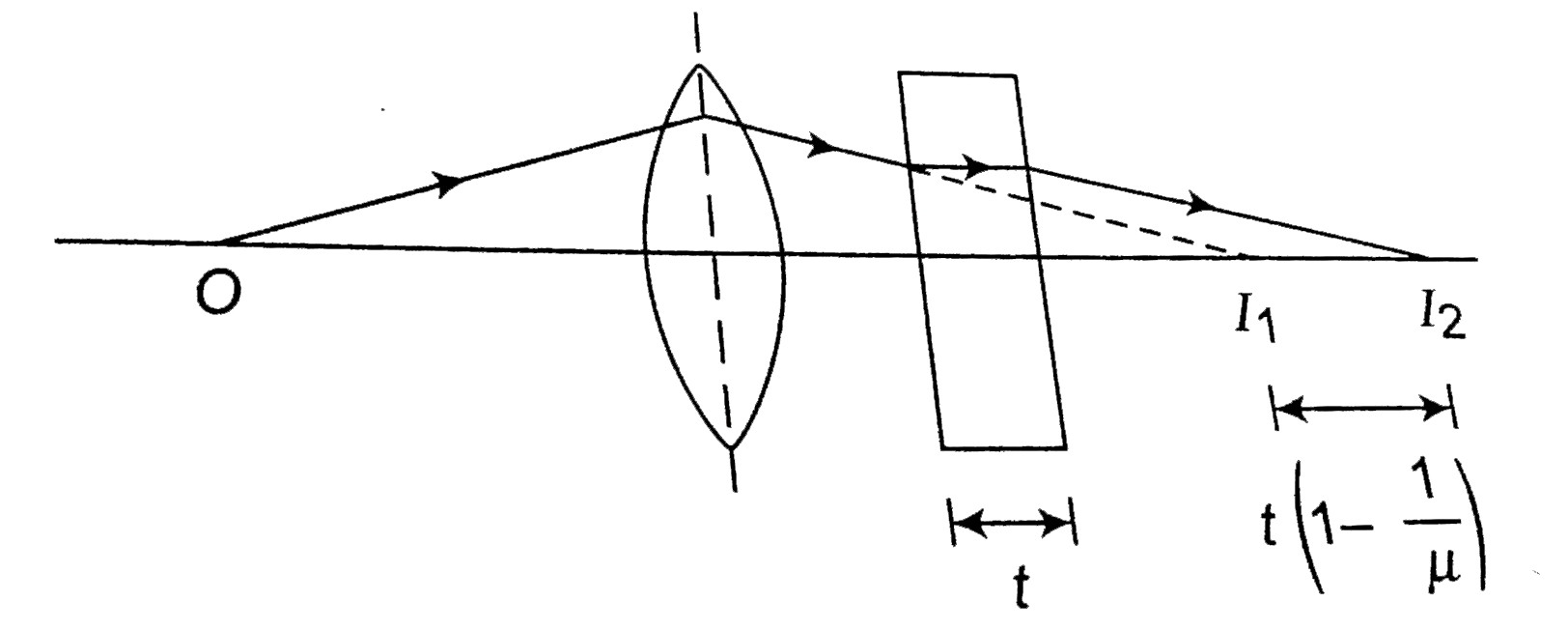
Shift of image by slab:
t(1−1μ)=t(μ−1μ) away from lens
Topper's Solved these Questions
- REFRACTION AT SPHERICAL SURFACESBOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES
105 Videos
- REFLECTION OF LIGHTBOOK - CP SINGHCHAPTER - REFLECTION OF LIGHTEXERCISE - EXERCISES
67 Videos
- REFRACTION OF LIGHT BY PLANE SURFACESBOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises
110 Videos
Similar Questions
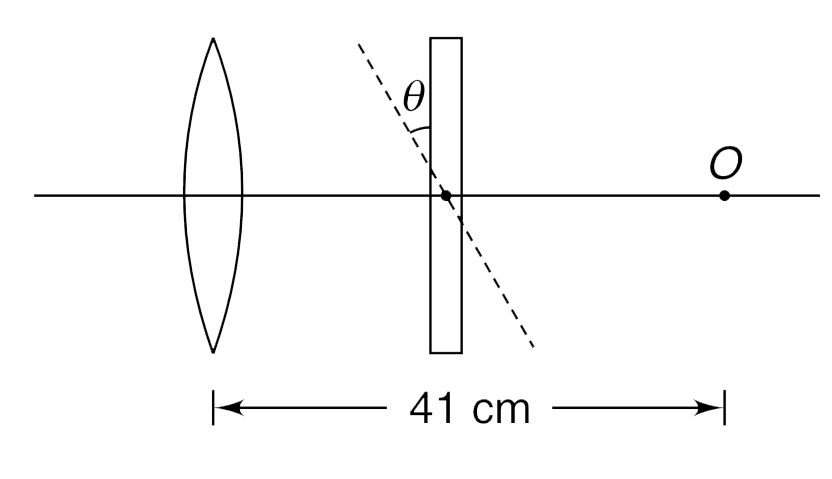
A point object O is placed at a distance of 41 cm from a convex lens of focal length f=20 cm on its principal axis. A glass slab of thickness 3 cm and refractive index μ=1.5 is placed between the lens and the object with its faces perpendicular to the principal axis of the lens. Image of the object is formed at point I1. Now the glass slab is tilted by an angle of θ=1° (as shown in the Figure) and the final image is formed at I2. Calculate the distance between points I1 and I2. Consider only paraxial rays for the lens and near normal incidence for the glass slab.
View SolutionAn object 240 cm in front of a lens forms a sharp image on a screen 12 cm behind the lens. A glass slab 1 cm thick, having refractive index 1.50 is placed between the lens and the screen with its refracting faces perpendicular to the principal axis of the lens.
(a) By how much distance the object must be moved so as to again cast a sharp image on the screen?
(b) Another identical glass slab is interposed between the object and the lens. How much further the object shall be moved so as to form a sharp image on the screen.
View Solution
Knowledge Check
P is a point on the axis of a concave mirror. The image of P, formed by the mirror, coincides with P. A rectangular glass slab of thickness t and refractive index μ is now introduced between P and the mirror. For the image of P to coincide with P again, the mirror must be moved
Atowards P by (μ−1)tBaway from P by (μ−1)tCaway from P by t(1−1μ)Dtowards P by t(1−1μ)A parallel beam of light is incident on a lens of focal length 10cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. The nature of the final image from the lens slab combination is: (Assume rays paraxial)
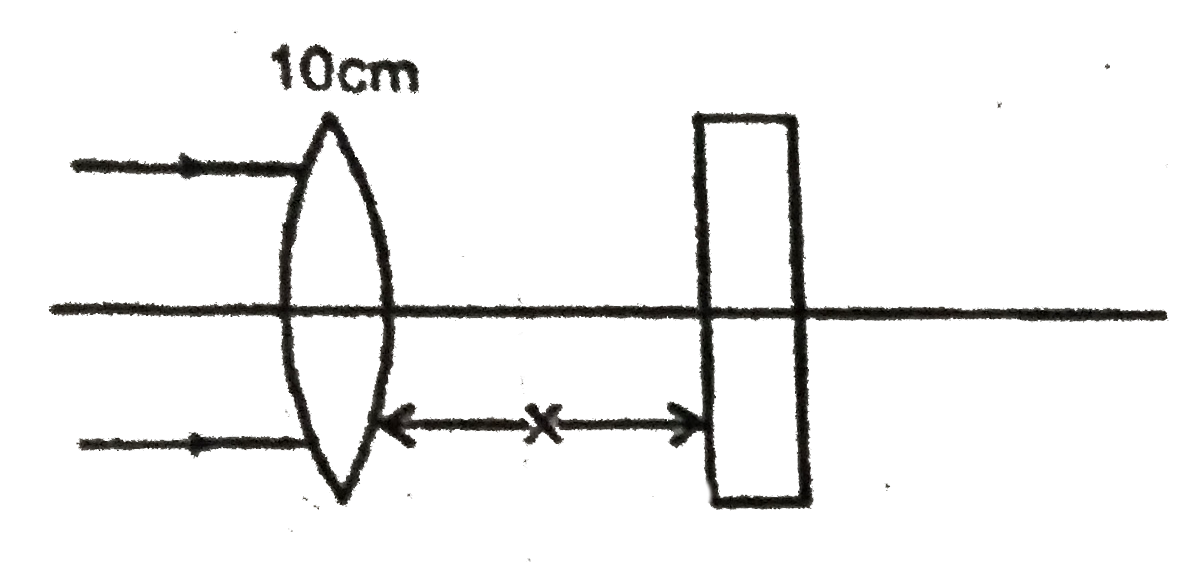 AAt distance of 11 cm and image is vertual if X=12 cmBAt distance of 11 cm and image virtual if X=14 cmCAt the Distance of 11 cm and image is virtual if X=16 cmDAll of the above
AAt distance of 11 cm and image is vertual if X=12 cmBAt distance of 11 cm and image virtual if X=14 cmCAt the Distance of 11 cm and image is virtual if X=16 cmDAll of the aboveA convex lens form a real image of a point object placed on its principal axis. If the upper half of the lens is painted black, the image will
ABe shifted downwardsBBe shifted upwardsCNot be shiftedDShift on the principal axis
A parallel beam of light is incident on a lens of focal length 10 cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. Find the distance of the final image from the lens.
 .
.
View SolutionA point object is placed at a distance of 25cm from a convex lens. Its focal length is 22cm. A glass slab of refractive index 1.5 is inserted between the lens and the object, then the image is formed at infinity. Find the thickness of the glass slab (in cm).
View SolutionA point object is placed at a distance of25cmfrom a convex lens of focal length 20cm.If a glass slab of thicknesstand refractive index 1.5is inserted between the lens and object.The image is formed at infinity .Find the thickness?
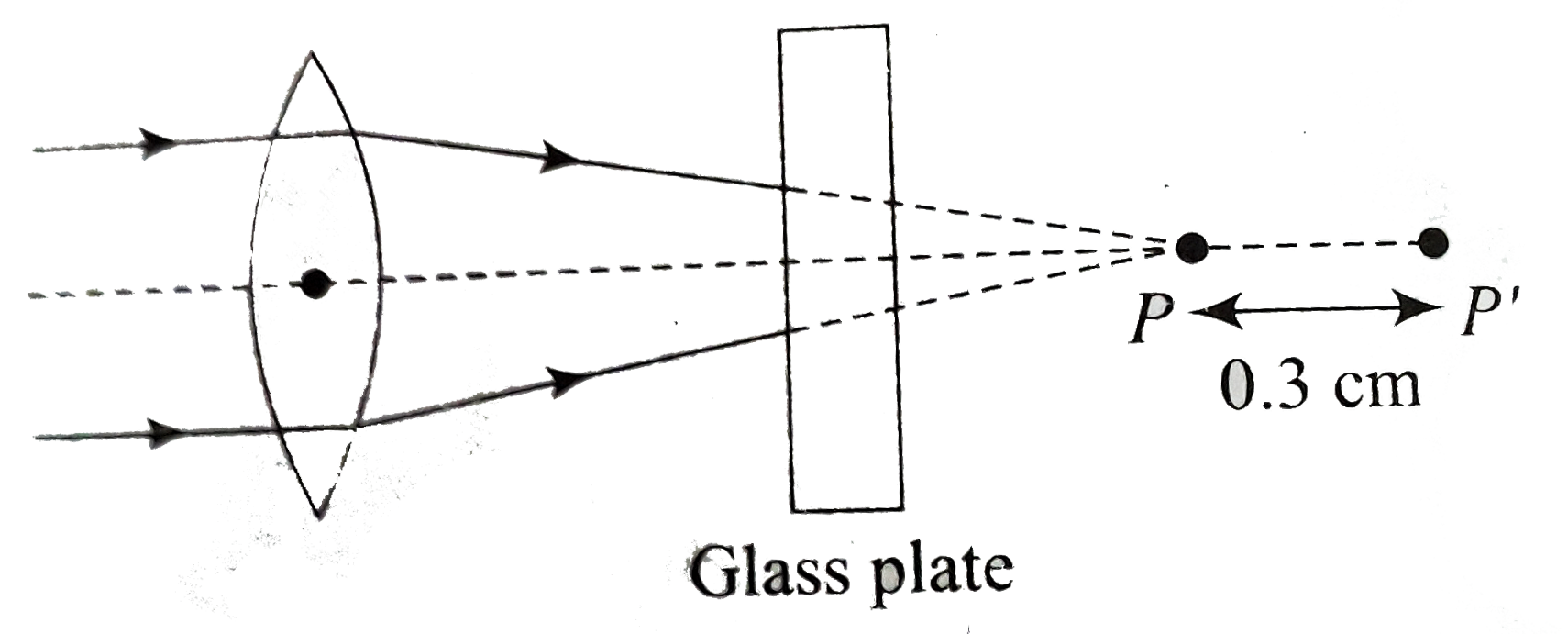
View SolutionRays from a lens are converging toward a point P, a shown in Figure. How much thick glass plate having refractive index 1.6 must be located between the lens and point P, so that the image will be formed at P′?
View SolutionA convex forms a real image of a poinnt object placed on its principal axis. If the upper half of the lens is painted black
View Solution
