If m = magnetic quantum number and l = azimuthal quantum number then :-
m=l+2
m=2l2+1
l=m−12
l=2m+1
The correct Answer is:C
To solve the question regarding the relationship between the magnetic quantum number (m) and the azimuthal quantum number (l), we will follow these steps:
1. Understanding Quantum Numbers:
- The azimuthal quantum number (l) determines the shape of the orbital and can take on integer values starting from 0. The possible values of l are:
- l = 0 (s orbital)
- l = 1 (p orbital)
- l = 2 (d orbital)
- l = 3 (f orbital)
2. Determining the Magnetic Quantum Number (m):
- The magnetic quantum number (m) describes the orientation of the orbital in space. The values of m depend on l and range from -l to +l, including zero. Thus, for a given l:
- For l = 0, m = 0 (1 value)
- For l = 1, m = -1, 0, +1 (3 values)
- For l = 2, m = -2, -1, 0, +1, +2 (5 values)
- For l = 3, m = -3, -2, -1, 0, +1, +2, +3 (7 values)
3. Finding the Relationship:
- The relationship between m and l can be expressed mathematically as:
m=2l+1
- This means that for any given value of l, the corresponding value of m can be calculated.
4. Rearranging the Equation:
- To find l in terms of m, we can rearrange the equation:
l=m−12
5. Conclusion:
- From the relationship m=2l+1, we can conclude that if we know the value of m, we can find l using the rearranged formula l=m−12.
Final Answer:
The relationship between the magnetic quantum number (m) and the azimuthal quantum number (l) is given by:
m=2l+1
And rearranging gives:
l=m−12
- The azimuthal quantum number (l) determines the shape of the orbital and can take on integer values starting from 0. The possible values of l are:
- l = 0 (s orbital)
- l = 1 (p orbital)
- l = 2 (d orbital)
- l = 3 (f orbital)
- The magnetic quantum number (m) describes the orientation of the orbital in space. The values of m depend on l and range from -l to +l, including zero. Thus, for a given l:
- For l = 0, m = 0 (1 value)
- For l = 1, m = -1, 0, +1 (3 values)
- For l = 2, m = -2, -1, 0, +1, +2 (5 values)
- For l = 3, m = -3, -2, -1, 0, +1, +2, +3 (7 values)
- The relationship between m and l can be expressed mathematically as:
m=2l+1
- This means that for any given value of l, the corresponding value of m can be calculated.
- To find l in terms of m, we can rearrange the equation:
l=m−12
- From the relationship m=2l+1, we can conclude that if we know the value of m, we can find l using the rearranged formula l=m−12.
The relationship between the magnetic quantum number (m) and the azimuthal quantum number (l) is given by:
m=2l+1
And rearranging gives:
l=m−12
Topper's Solved these Questions
- ATOMIC STRUCTUREBook:ALLENChapter:ATOMIC STRUCTUREExercise:Exercise - 03
Explore 22 Videos
- ATOMIC STRUCTUREBook:ALLENChapter:ATOMIC STRUCTUREExercise:Exercise - 04[A]
Explore 51 Videos
- ATOMIC STRUCTUREBook:ALLENChapter:ATOMIC STRUCTUREExercise:Exercise - 01
Explore 38 Videos
- IUPAC NOMENCLATUREBook:ALLENChapter:IUPAC NOMENCLATUREExercise:Exercise - 05(B)
Explore 8 Videos
Similar Questions
Knowledge Check
Azimuthal quantum number defines.
Ae/m ratio of electronBspin of electronCangular momentum of electronDmagnetic momentum of electronicAzimuthal quantum number determines the
AsizeBspinCorientationDangular momentum of orbitalsThe total number of electrons that can be accommodated in all the orbitals having principal quantum number 2 and azimuthal quantum number 1 are
A2B4C6D8
Magnetic Quantum Number & Orbital
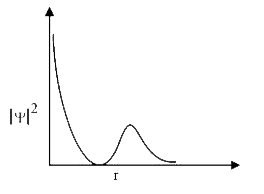
View SolutionThe graph for an orbital between |φ|2 and r(radial distance) is shown below. The sum of principle quantum number, azimuthal, quantum number and magnetic quantum number of this orbital is ____________.
View SolutionIn the modern periodic table, the period indicates the value of
a. atomic number
b.atomic mass
c.principal quantum number
d.azimuthal quantum number
View SolutionThe total number of electrons that can be accommodated in all orbitals having principal quantum number 2 and azimuthal in quantum number 1 is
View SolutionAzimuthal Quantum number was given by
View Solution