Find the median of the following data: 19, 25, 59, 48, 35, 31, 30, 32, 51. If 25 is replaced by 52 , what will be the new median.
To find the median of the given data set and determine the new median after replacing a number, we can follow these steps:
Step 1: Arrange the data in ascending order
The original data set is:
19,25,59,48,35,31,30,32,51
Arranging it in ascending order gives:
19,25,30,31,32,35,48,51,59
Step 2: Count the number of data points
Count the number of values in the ordered data set. Here, we have:
- Total numbers (n) = 9
Step 3: Find the median
Since the number of data points (n) is odd, the median is the middle number. The formula for finding the median when n is odd is:
\( \text{Median} = \text{Value at position} \left( \frac{n + 1}{2} \right) \)
Calculating the position:
\( \frac{9 + 1}{2} = 5 \)
So, the median is the 5th number in the ordered list.
From the ordered data:
- The 5th number is 32.
Thus, the median of the original data set is:
Median = 32
Step 4: Replace 25 with 52
Now, we replace 25 with 52 in the original data set. The new data set becomes:
19,52,59,48,35,31,30,32,51
Step 5: Arrange the new data in ascending order
Arranging the new data set gives:
19,30,31,32,35,48,51,52,59
Step 6: Count the number of data points again
The count remains the same:
- Total numbers (n) = 9
Step 7: Find the new median
Again, since the number of data points (n) is odd, we use the same median formula:
\( \text{Median} = \text{Value at position} \left( \frac{n + 1}{2} \right) \)
Calculating the position:
\( \frac{9 + 1}{2} = 5 \)
So, the median is the 5th number in the new ordered list.
From the new ordered data:
- The 5th number is 35.
Thus, the new median after replacing 25 with 52 is:
New Median = 35
Summary of Results
- Original Median = 32
- New Median = 35
---
The original data set is:
19,25,59,48,35,31,30,32,51
19,25,30,31,32,35,48,51,59
Count the number of values in the ordered data set. Here, we have:
- Total numbers (n) = 9
Since the number of data points (n) is odd, the median is the middle number. The formula for finding the median when n is odd is:
\( \text{Median} = \text{Value at position} \left( \frac{n + 1}{2} \right) \)
\( \frac{9 + 1}{2} = 5 \)
So, the median is the 5th number in the ordered list.
- The 5th number is 32.
Median = 32
Now, we replace 25 with 52 in the original data set. The new data set becomes:
19,52,59,48,35,31,30,32,51
Arranging the new data set gives:
19,30,31,32,35,48,51,52,59
The count remains the same:
- Total numbers (n) = 9
Again, since the number of data points (n) is odd, we use the same median formula:
\( \text{Median} = \text{Value at position} \left( \frac{n + 1}{2} \right) \)
\( \frac{9 + 1}{2} = 5 \)
So, the median is the 5th number in the new ordered list.
- The 5th number is 35.
New Median = 35
- Original Median = 32
- New Median = 35
Topper's Solved these Questions
Similar Questions
Find the median for the following data :

View SolutionFind the median for the following data :

View SolutionFind the median for the following data.

View SolutionFind the median from the following data :
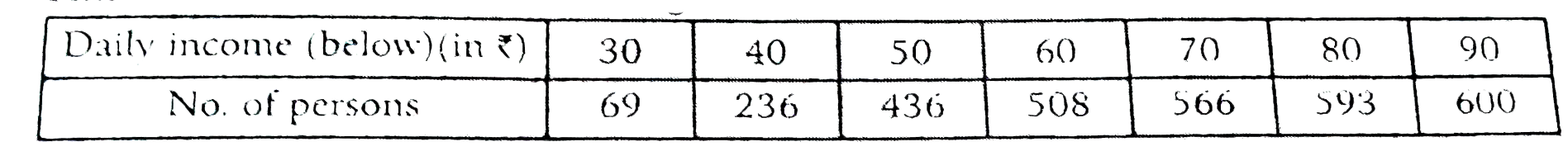
View SolutionFind the median from the following data :

View SolutionFind the median from the following data :
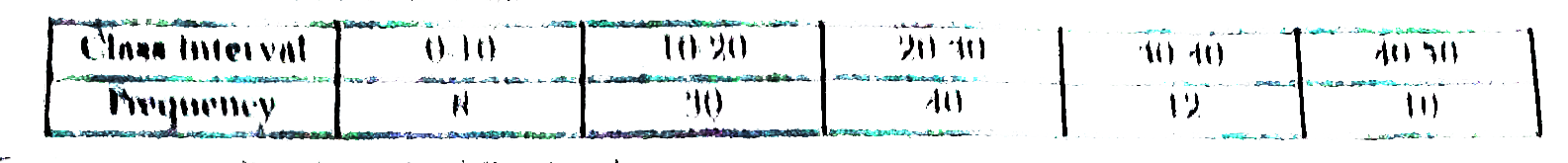
View SolutionFind the median from the following data :
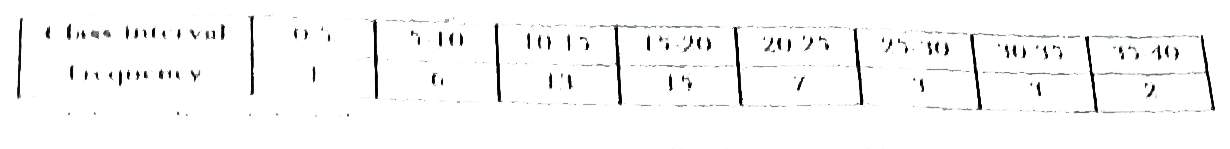
View SolutionFind the median from the following data :
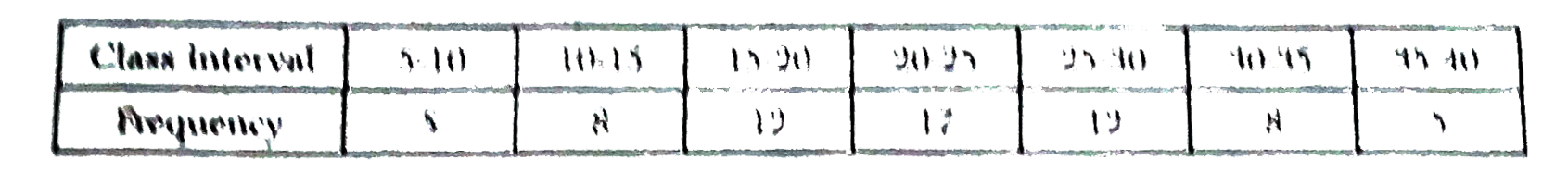
View SolutionFind the median from the following data :

View SolutionFind the median from the following data :

View Solution
