_S01_020_Q01.png)
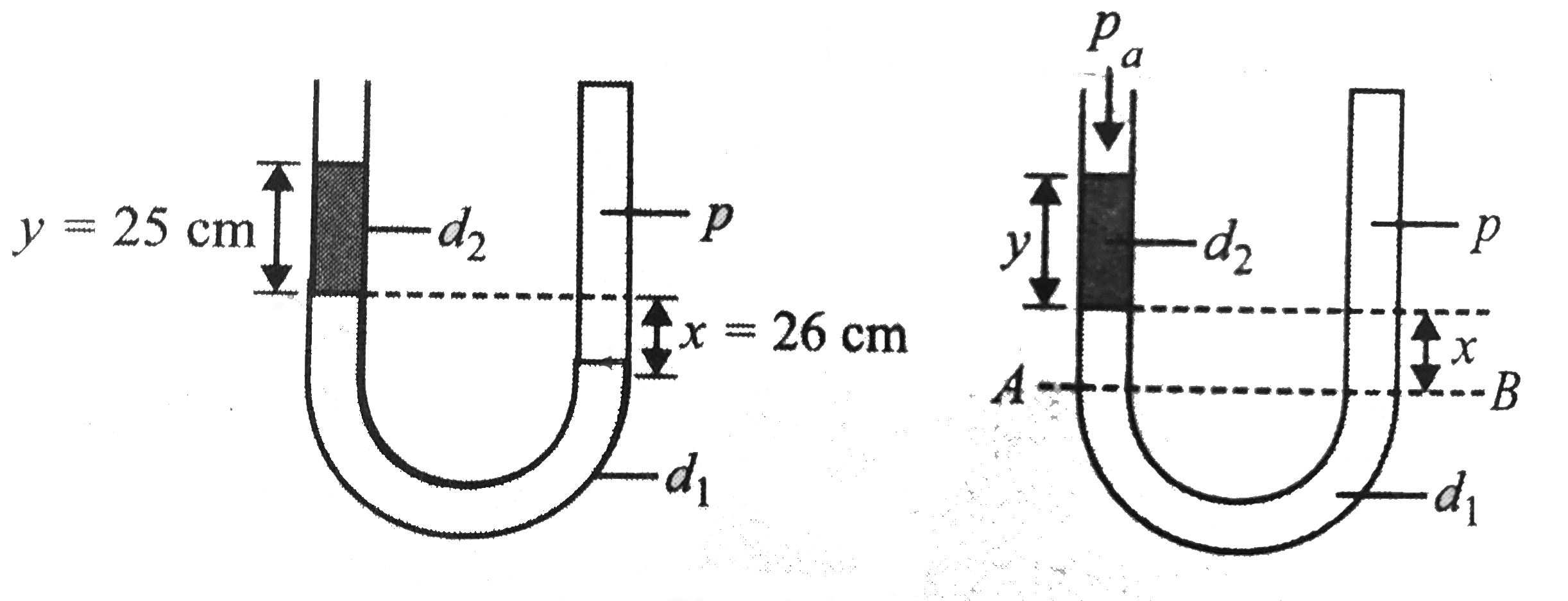
In a given U-tube (open at one-end) find out relation between p and pa
Given d2=2×13.6gm/cm3,d1=13.6gm/cm3
_S01_020_S01.png)
pressure in a liquid at same level is same i.e., A-A-
In C.G.S pa+d2yd+xd1g=p
pa+13.6×2×25×g+13.6×26×g=p
pa+13.6×g[50+26]=p
⇒2pa=p as p∘=13.6×g×76
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Elasticity)16videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Surface Tension)21videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
Similar Questions
Knowledge Check
- Question 1 - Select One
An ideal gas is collected by downward displacement of water. Select the correct expression for Pgas according to the diagram [dHg=13.6g/cm3]:
 APgas=Patm−[aq. Tension+h13.6]BPgas=Patm−hdgCPgas=Patm+hdgDPgas=Patm−aq. Tension+h13.6
APgas=Patm−[aq. Tension+h13.6]BPgas=Patm−hdgCPgas=Patm+hdgDPgas=Patm−aq. Tension+h13.6 - Question 2 - Select One
The domain of the relation
R={(1,3),(3,5),(2,6)} isA1,3and2B{1,3,2}C{3,5,6}D3,5and6
In the arrangement shown in figure a viscous liquid whose density is 1gm/cm3 flows along a tube out of a wide tank A. Find the velocity of the liquid flow if h1=10cm,h2=20cm,h3=35cm. All the distances l are equal.
 View Solution
View SolutionGiven two independent events A and B such that P(A)=0.3 and P(B)=0.6 . Find: P(B/A)
View SolutionGiven two independent events A and B such that P(A)=0.3 and P(B)=0.6 . Find: P(A∩B)
View SolutionGiven two independent events A and B such that P(A)=0.3 and P(B)=0.6 . Find: P(A∪B)
View SolutionGiven two independent events A and B such that P(A)=0.3 and P(B)=0.6 . Find: P(A/B)
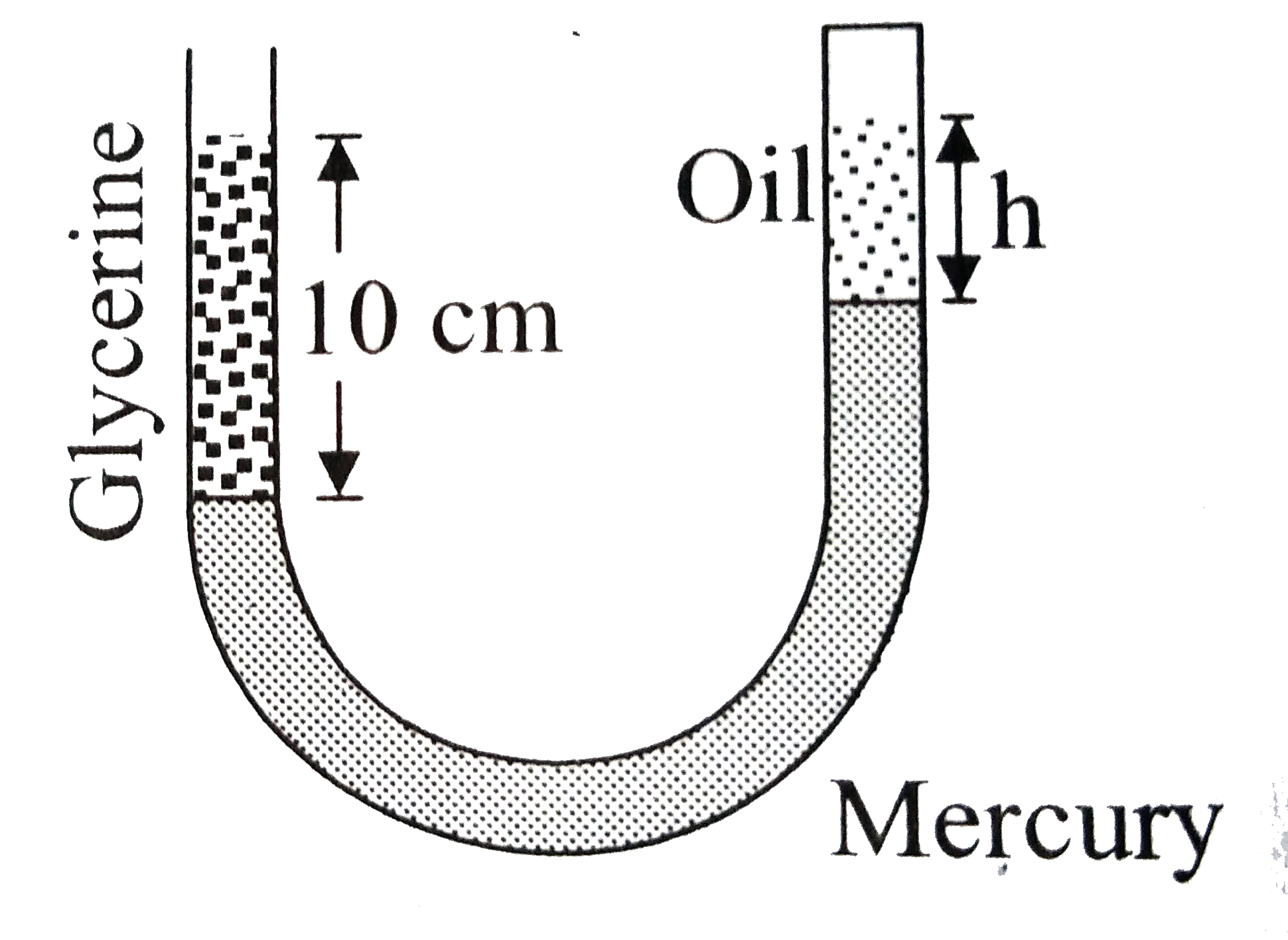
View SolutionA vertical U-tube of uniform inner cross section contains mercury in both sides of its arms. A glycerin (density =1.3g/cm3) column of length 10 cm is introduced into one of its arms. Oil of density 0.8 gm/cm3 is poured into the other arm until the upper surfaces of the oil and glycerin are in the same horizontal level. Find the length of the same horizontal level. Find the length of the oil column, Density of mercury =13.6g/cm3
 View Solution
View Solution