_E01_021_Q01.png)
The adjoining diagram shows three soap bubbles, A , B and C prepared by blowing the capillary tube fitted with stop cocks S, S1,S2 and S3 with stop cock S closed and stop cocks S1,S2 and S3 opened-
B will start collapsing with volumes of A and C increasing
C will start collapsing with volumes of A and B increasing
C and A will both start collapsing with the volume of B increasing
volumes of A, B and C will become equal to equilibrium.
The correct Answer is:C
Step by step video, text & image solution for The adjoining diagram shows three soap bubbles, A , B and C prepared by blowing the capillary tube fitted with stop cocks S, S_(1),S_(2) and S_(3) with stop cock S closed and stop cocks S_(1),S_(2) and S_(3) opened- by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Fluid Statics)40videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 2 (One or more than one correct answer)53videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Elasticity)16videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
Similar Questions
The resistors R1,R2,R3 and R4 are connected as shown in the figure. S1 and S2 are two switches . Discuss the flow of current through the resistors when
(1) S1 and S2 both are closed.
(2) S1 and S2 both are open.
(3) S1 is closed and S2 in open.
View SolutionGourang made an electric circuit with three bulbs B1,B2 and B3 a cell and two switches S1 and S2 as shown in figure. He notes his observation when
(a) S1 is closed and S2 is open,
(b) S2 is closed and S1 is open.
He also found that a bulb whose failure made the circuit 'open' irrespective of the status of S1 and S2 . What are his observation.View Solution
Knowledge Check
- Question 1 - Select One
The following diagram shows three metal balls Ball A is charged to Q coulombs and B,C are unchanged .The charges on balls B,C when the switches S1 and S2 are closed are respectively
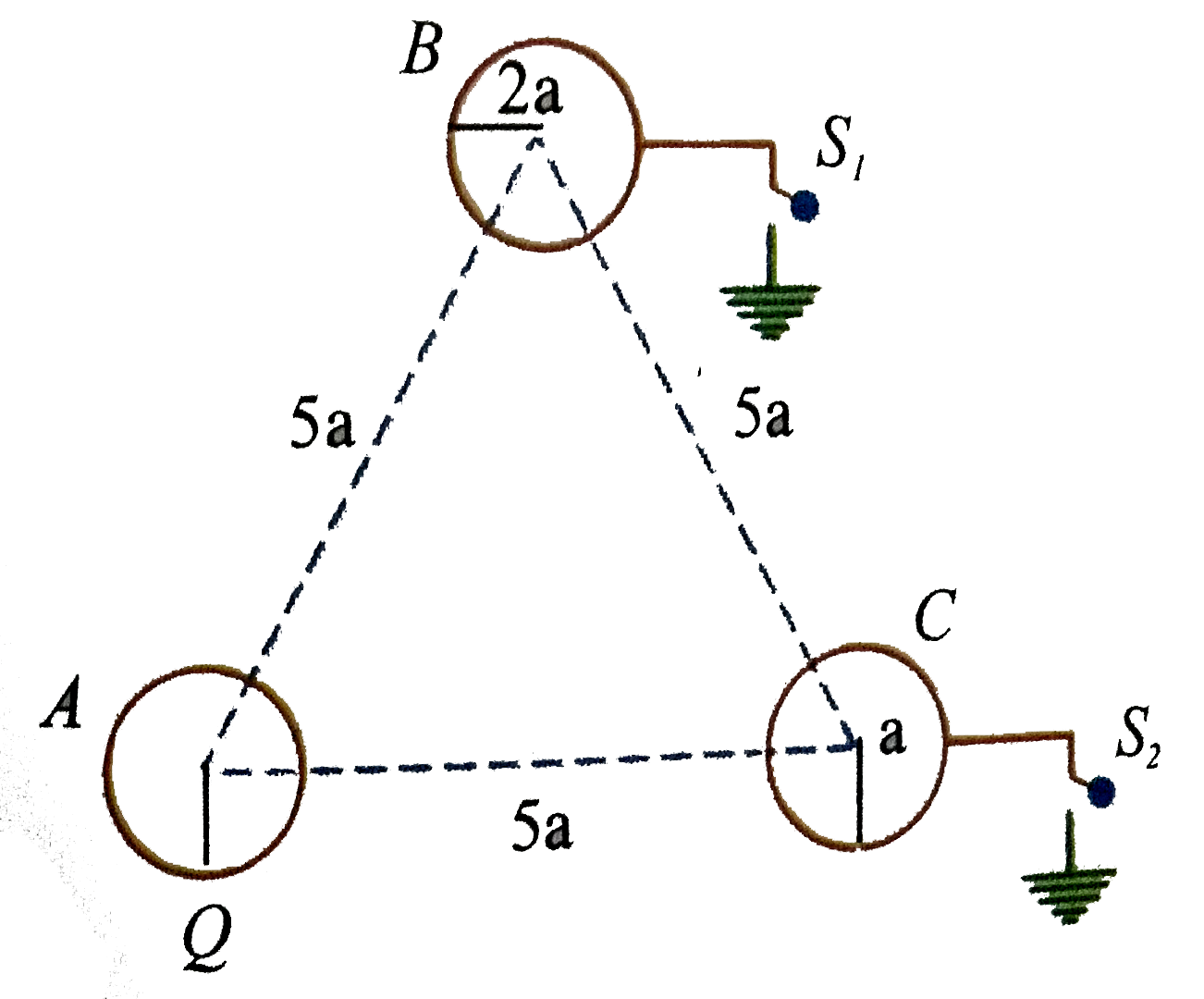A8Q23,3Q23B3Q23,8Q23,C−8Q23,−3Q23D−3Q23,−8Q23 - Question 2 - Select One
If S1,S2,S3 are the sums of n, 2n, 3n terms respectively of an A.P., then S3/(S2−S1)−
A1B2C3D4 - Question 3 - Select One
Let each of the circles
S1≡x2+y2+4y−1=0
S1≡x2+y2+6x+y+8=0
S3≡x2+y2−4x−4y−37=0
touch the other two. Also, let P1,P2 and P3 be the points of contact of S1 and S2,S2 and S3, and S3 , respectively, C1,C2 and C3 are the centres of S1,S2 and S3 respectively.
P2 and P3 are images of each other with respect to the lineAy=xBy=−xCy=x+1Dy=−x+2
In the given figure switches S1andS2 are in open condition. The resistance across ab when the switches S1andS2 are closed is ……………… Ω.
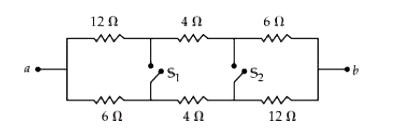View SolutionThe stopping potential eVs depends on
View SolutionGourang made an electric circuit with three bulbs B1,B2 and B3 a cell and two switches S1 and S2 as shown in figure. He notes his observation when
(a) S1 is closed and S2 is open,
(b) S2 is closed and S1 is open.
He also found that a bulb whose failure made the circuit 'open' irrespective of the status of S1 and S2 . What are his observation.View SolutionLet each of the circles
S1≡x2+y2+4y−1=0
S1≡x2+y2+6x+y+8=0
S3≡x2+y2−4x−4y−37=0
touch the other two. Also, let P1,P2 and P3 be the points of contact of S1 and S2,S2 and S3, and S3 , respectively, C1,C2 and C3 are the centres of S1,S2 and S3 respectively.
The coordinates of P1 areView Solution_E01_054_Q01.png)
A monochromatic light source of wavelength λ is placed at S. three slits S1,S2 and S3 are equidistant from the source S and the point P on the screen S1P−S2P=λ/6 and S1P−S3P=2λ/3. if I be the intensity at P when only one slit is open the intensity at P when all the three slits are open is-View Solution