The side of glass aquarium is 1 m high and 2m long, when the aquarium is filled to the top with water what is the total force against the side-
980×103N
9.8×103N
0.98×103N
0.098×103N
The correct Answer is:B
To solve the problem of finding the total force against the side of a glass aquarium filled with water, we can follow these steps:
1. Identify the Dimensions:
- The height (h) of the aquarium is 1 meter.
- The length (L) of the aquarium is 2 meters.
2. Understand the Pressure at a Depth:
- The pressure (P) at a depth y in a fluid is given by the formula:
P=ρgy
where:
- ρ = density of water (approximately 1000kg/m3)
- g = acceleration due to gravity (approximately 9.8m/s2)
- y = depth from the surface of the water.
3. Calculate the Force on a Differential Strip:
- Consider a small horizontal strip of height dy at depth y.
- The area (dA) of this strip is:
dA=L⋅dy=2m⋅dy
- The differential force (dF) acting on this strip is:
dF=P⋅dA=(ρgy)⋅(2dy)=2ρgydy
4. Integrate to Find Total Force:
- To find the total force (F) against the side of the aquarium, integrate dF from y=0 to y=1:
F=∫10dF=∫102ρgydy
- This integral can be computed as follows:
F=2ρg∫10ydy=2ρg(y22)10=2ρg⋅122=ρg
5. Substitute Values:
- Now substitute the values of ρ and g:
F=1000kg/m3⋅9.8m/s2=9800N
6. Final Result:
- The total force against the side of the aquarium is:
F=9800N
- The height (h) of the aquarium is 1 meter.
- The length (L) of the aquarium is 2 meters.
- The pressure (P) at a depth y in a fluid is given by the formula:
P=ρgy
where:
- ρ = density of water (approximately 1000kg/m3)
- g = acceleration due to gravity (approximately 9.8m/s2)
- y = depth from the surface of the water.
- Consider a small horizontal strip of height dy at depth y.
- The area (dA) of this strip is:
dA=L⋅dy=2m⋅dy
- The differential force (dF) acting on this strip is:
dF=P⋅dA=(ρgy)⋅(2dy)=2ρgydy
- To find the total force (F) against the side of the aquarium, integrate dF from y=0 to y=1:
F=∫10dF=∫102ρgydy
- This integral can be computed as follows:
F=2ρg∫10ydy=2ρg(y22)10=2ρg⋅122=ρg
- Now substitute the values of ρ and g:
F=1000kg/m3⋅9.8m/s2=9800N
- The total force against the side of the aquarium is:
F=9800N
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 2 (One or more than one correct answer)53videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Assertion & Reason)32videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Surface Tension)21videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
Similar Questions
Two men on either side of a tower 75 m high observe the angle of elevation of the top of the tower to be 30° and 60°. What is the distance between the two men ?
View SolutionThe L-shaped fish tank shown in Fig. is filled with water and is open at the top . Here , d = 70 m .
(a) What is the (total) force exerted by the water on face A ?
(b) What is the (total) force exerted by the water on face B ?
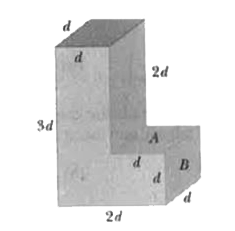 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The dimensions of a rectangular vessel are 2m×2m×1m. lt is completely filled with water. What is the total force acting against any vertical face ?
[ρwater=103kg/m3A4.9×103NB9.8×103 NC7.5×102 ND12.5×103 N - Question 2 - Select One
Two sides of a triangle are 6 m and 8 m long , and angle between them is increasing at the rate of 2∘ per sec. When the angle between them is 60∘, the third side is increasing at the rate of
A2π5√39m/sB5π2√39m/sC2√395πm/sD10π√39m/s - Question 3 - Select One
A field is in the shape of a trapezium whoseparallel sides are 200 m and 400 m long, whereas each of other two sides is 260 m long. What is the area (in m2)of the field?
A78000B52000C72000D60000
A ladder 13 m long reaches a window which is 12 m above the ground on side of a street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 5m high, then the width of the street is:
View SolutionA ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
View SolutionA large aquarium of height 5.00 m is filled with fresh water to a depth of 2.00 m. One wall of the aquarium consists of thick plastic 9.00 m wide. By how much does the total force on that wall increase if the aquarium is next filled to a depth of 4.00 m?
View SolutionA rectangular water tank is 5 m high, 3 m long and 2 m wide. How many litres of water can it hold?
View SolutionThe floor of a rectangular room is 15 m long and 12 m wide. The room is surrounded by a verandah of width 2 m on all its sides. The area of the verandah is:
View Solution

