_S01_013_Q01.png)
A very small groove is made in the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle fro that place.
_S01_013_S01.png)
Suppose we project the particle with speed ve
so that it just reaches at (r→∞)
Applying energy conservation Ki+Ui=Kf+Uf
12m0v2e+m0[−GMe2R3{3R2−(R2)2}]=0
⇒ve=√11GMe4R
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 1 (Check your Grasp)28videos
GRAVITATION
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 2 (Brain Teasers)27videos
GRAVITATION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)48videos
KINEMATICS-2D
Similar Questions
a narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.
 View Solution
View SolutionAssume that a tunnel is dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless.
(a) Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel.
(b) Find the component of this force along the tunnel and perpendicular to the tunnel.
(c) Find the normal force exerted by the wall on the particle.
(d) Find the resultant force on the particles.
(e) Show that the motion of the particle in the tunnel is simple harmonic and find the time period.View Solution
Knowledge Check
- Question 1 - Select One
A table with smooth horiztonal surface is truning at an angular speed ω abouyt its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.
Av=ω2(L2−a2)13Bv=ω(L2−a2)Cv=ω2√L2−a2Dv=ω√L2−a2 - Question 2 - Select One
A satellite of mass m is placed at a distance r from the centre of earth (mass M ). The mechanical energy of the satellite is
A−GMmrBGMmrCGMm2rD−GMm2r - Question 3 - Select One
A long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
A√qλlnrπm∈0B√qλln2πm∈0C√qλln22πm∈0D√qλln2πm∈0
A semicircular wire hs a length L and mass M. A paricle of mass m is placed at the centre of the circle. Find the gravitational attrction on the particle due to the wire.
View SolutionA tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionAssume that a tunnel ils dug along a chord of the earth, at a perpendicular distance R/2 from the earth's centre where R is the radius of the earth. The wall of the tunnel is frictionless. a. Find the gravitational force exerted by the earth on a particle of mass m placed in the tunnel at a distance x from the centre of the tunnel. b. Find the component of this fore along the tunnel and perpendicular to the tunnel. c. Find the normal force exerted by the wall on the particle. d. Find the resultant force on the particle. e.Show that the motion of the particle in the tunnel is simple harmonic and find the time period.
View Solution(a) A tunnel is dug along a diameter of the earth. Find the force on the a particle of mass m placed in the tunnel at a distance x from the centre.
(b) A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth's centre. the wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.View Solution(a) A uniform rod of mass M and length L is placed at distance L from a point mass m as shown. Find force on m
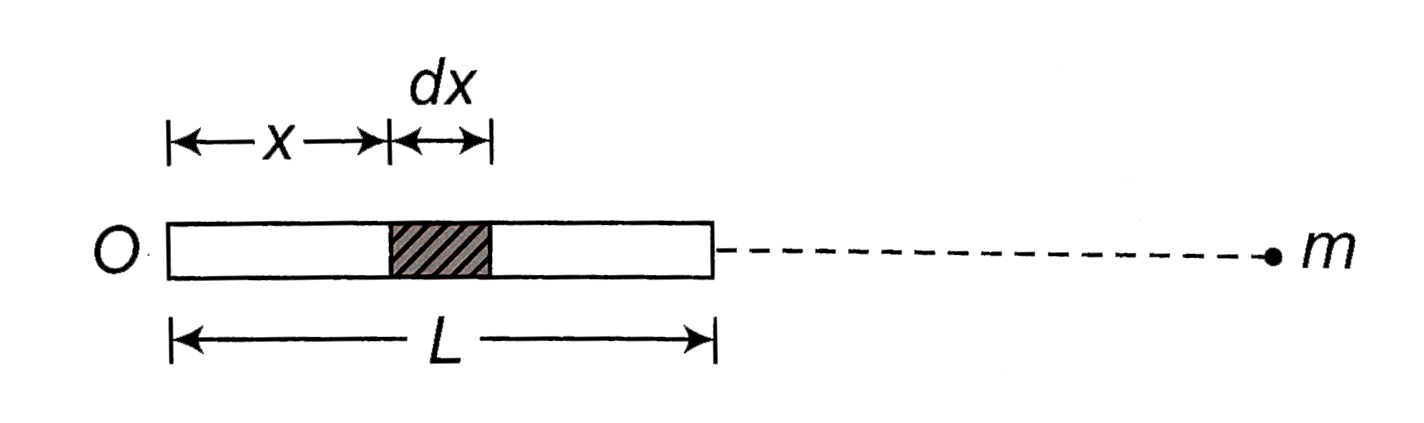
(b) A semiconductor wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. find the gravitational attraction on the particle due to the wire.View Solution

