Find the potential energy of the gravitational interation of a point mass of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line such that the point mass is at a distance 'a' from one end. Also find the force of their interaction.
The correct Answer is:−GMmlloge(1+la)
_E01_085_S01.png)
U=GM1M2d for the point mass
dU=GmdMx⇒U=−∫GMmlxdx
U=−GMml∫l+aadxx=−GMmlln(l+aa)
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 4 B (Brain Storming Subjective Exercise)
20 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 5 A (Previous Year Questions)
26 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 3 (Miscellaneous Type Questions)
20 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
48 Videos
Similar Questions
Find the potential energy of the gravitational interaction
(a) of two mass points of masses m1 and m2 located at a distance r from each other,
(b) of a mass point of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line at a distance a from each other, also find the force of their interaction.
View SolutionFind the potential V at P in the gravitational field of fixed point mass M.
View Solution
Knowledge Check
Choose the most appropriate option.
The potential energy of gravitational interaction of a point mass m and a thin uniform rod of mass M and length L, if they are located along a straight line at a distance a from each other, isAU=GMmaln(a+Lα)BU=GMm(1a−1a+L)CU=−GMmaDU=−GMmLln(a+La)Find the potential energy of the gravitational interaction of a point mass m and a rod of mass m and length l, if they are along a straight line. Point mass is at a distance of a from the end of the rod.

Find the potential energy of the gravitationalAU=−Gm2lln(2a+l2a−l)BU=−Gm2l2ln(2a+l2a−l)CU=−Gm2l2ln(2a−l2a+l)DU=−Gm2l2ln(2a−l2a+l)2The gravitational force of attraction between a uniform sphere of mass M and a uniform rod of length l and mass in as shown in figure is
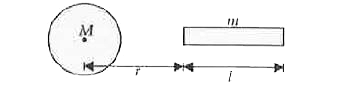 AGMmr(r+1)BGMr2CMm2D(r2+1)mM
AGMmr(r+1)BGMr2CMm2D(r2+1)mM
Find the M.I. of thin uniform rod of mass M and length L about the axis as shown.

View SolutionFind the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.

View SolutionFind the gravitational potential energy of a system consisting of a uniform rod AB of mass M, length l and a point mass m as shown in figure.
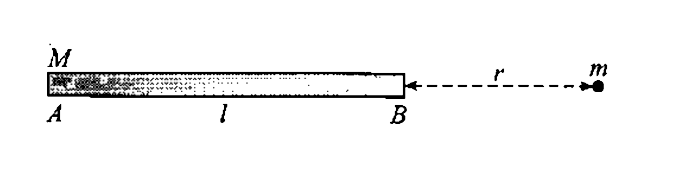
View SolutionFind the gravitational potential energy of system consisting of uniform rod AB of mass M, length l and a point mass m as shown in figure.

View SolutionFind the gravitatinal force of between a point mass m placed at a disance x on the prolongation of a thin rod of mass M andlength l from near end .
View Solution
