A particle is projected from gound At a height of 0.4 m from the ground, the velocity of a projective in vector form is →v=(6ˆi+2ˆj)m/s (the x-axis is horizontal and y-axis is vertically upwards). The angle of projection is (g=10m/s2)
45∘
60∘
30∘
tan−1(3/4)
The correct Answer is:C
Let u be the initial speed of the particle
Then v2=u2−2gh
or u2=v2+2gh
or u2x+u2y=v2x+v2y+2gh (vx=ux)
or u2y=v2y+2gh
or u2y=(2)2+(2)(10)(0.4)=12
therforeuy=√12 or 2√3m/s
and ux=vy=6m/s
and ux=vy=6m/s
∴θ=uyux=2√36=1√3
or θ=30∘.
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A particle is projected from ground with velocity 3ˆi+4ˆi m/s. Find range of the projectile :-
View SolutionVelocity of a projectile at height 15m from ground is v=(20ˆi+10ˆj)m/s. Here ˆi is in horizontal direction and ˆj is vertically upwards. Then
Speed with which particle is projected from ground is……… m/s
View Solution
Knowledge Check
At a height of 0.4 m from the ground, the velocity of projectile in vector from is →u=(6ˆi+2ˆj) (the x-axis is horizontal and y-axis is vertically upwards). The angle of projection is : (g=10m/s2)
A45∘B60∘C30∘Dtan−13/4Velocity of a projectile at height 15m from ground is v=(20ˆi+10ˆj)m/s. Here ˆi is in horizontal direction and ˆj is vertically upwards. Then
Angle of projectile with ground isA45∘B30∘C37∘D60∘Velocity of a projectile at height 15m from ground is v=(20ˆi+10ˆj)m/s. Here ˆi is in horizontal direction and ˆj is vertically upwards. Then
Horizontal range of the ground is …………mA60B50C80D70
Velocity of a projectile at height 15m from ground is v=(20ˆi+10ˆj)m/s. Here ˆi is in horizontal direction and ˆj is vertically upwards. Then
Maximum height from a ground is ……..m
View SolutionA particle is projected at an angle θ from ground with speed u (g = 10 m/s2 )
View SolutionA particle is projected from ground with velocity 40√2m/s at 45∘. At time t=2s
View SolutionTwo graphs of the same projectile motion (in the xy-plane) projected from origin are shown. X-axis is along horizontal direction and y-axis is vertically upwards. Take g=10ms−2.
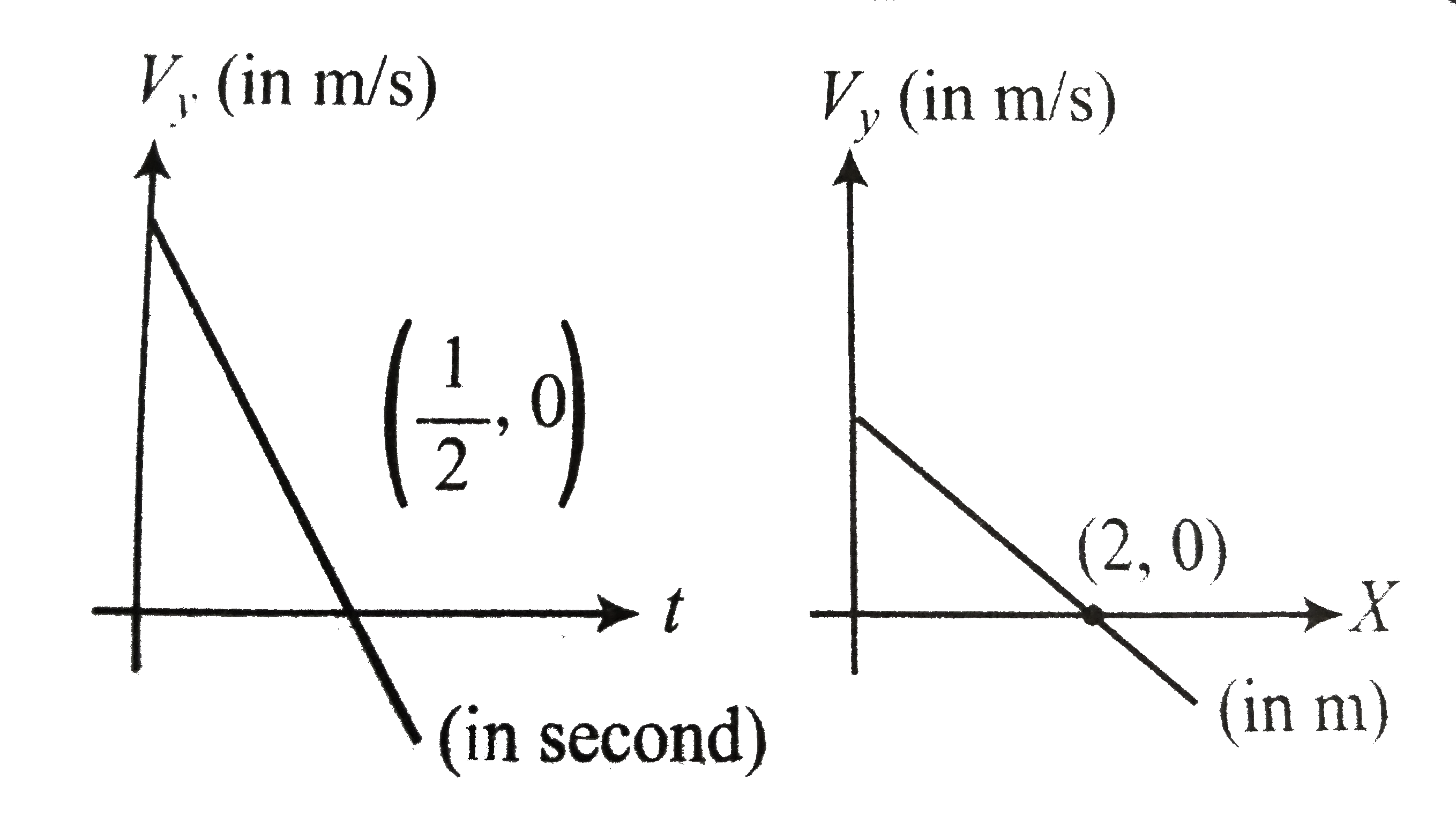 ,
,
The projection speed is :
View SolutionAssertion At height 20 m from ground , velocity of a projectile is v=(20ˆi+10ˆj)ms−1. Here, ˆi is horizontal and ˆj is vertical. Then, the particle is at the same height after 4s.
Reason Maximum height of particle from ground is 40m (take, g=10ms−2)
View Solution
