A body which was released from rest, slides down on an inclined plane of inclination θ. The coefficient of friction dowh the plane varies as μ=kx where k is a spositive constant and x is the distance moved by the body down the plane. The speed of the body 'v' versus distance 'x' graph will be as :

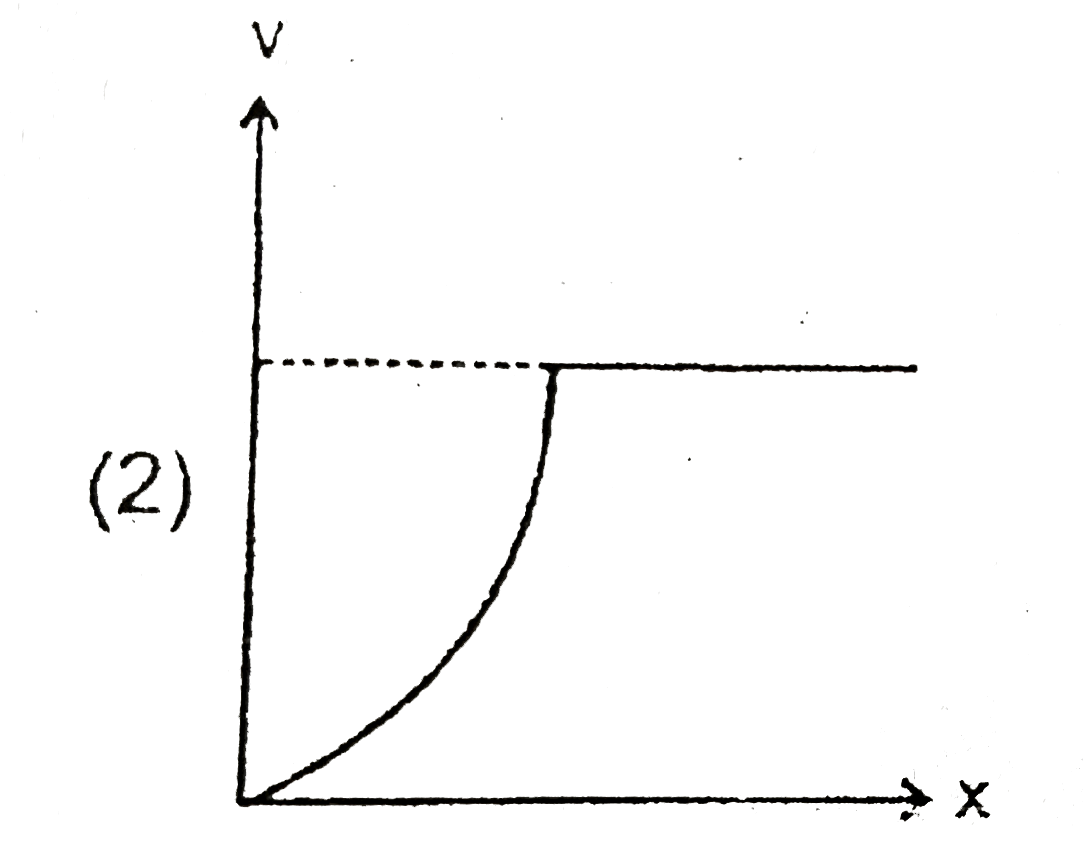
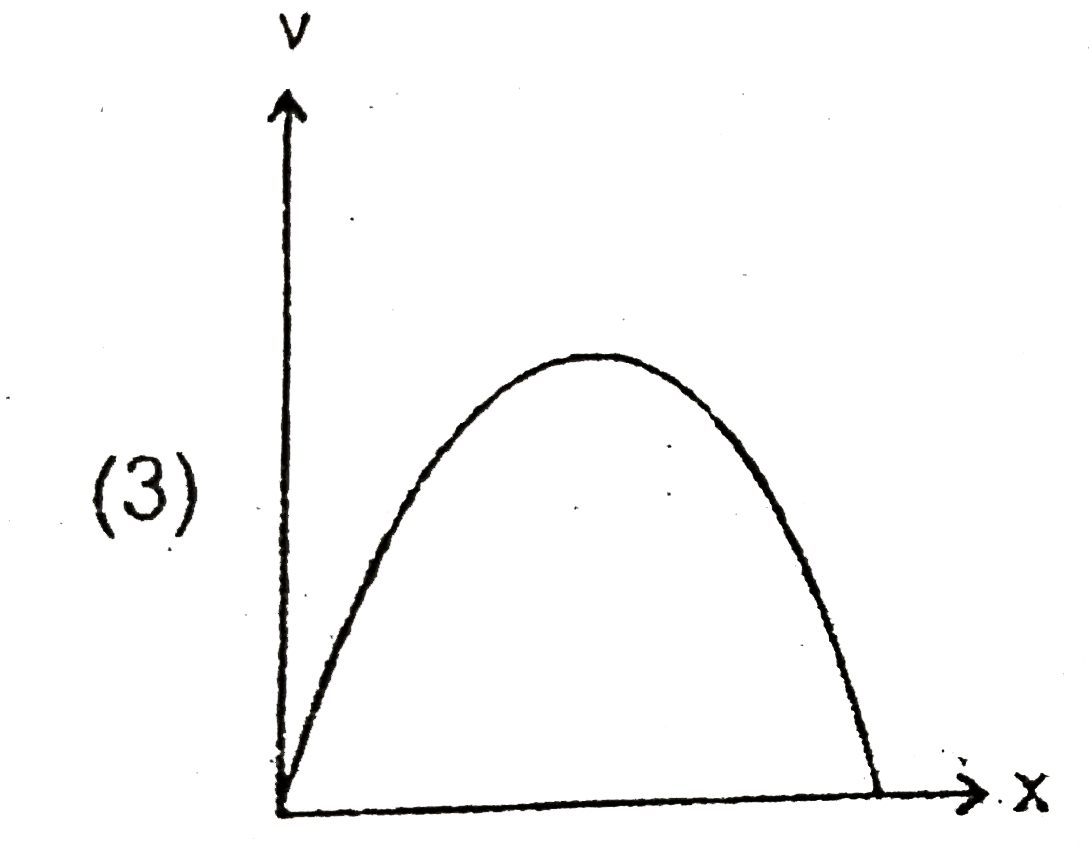
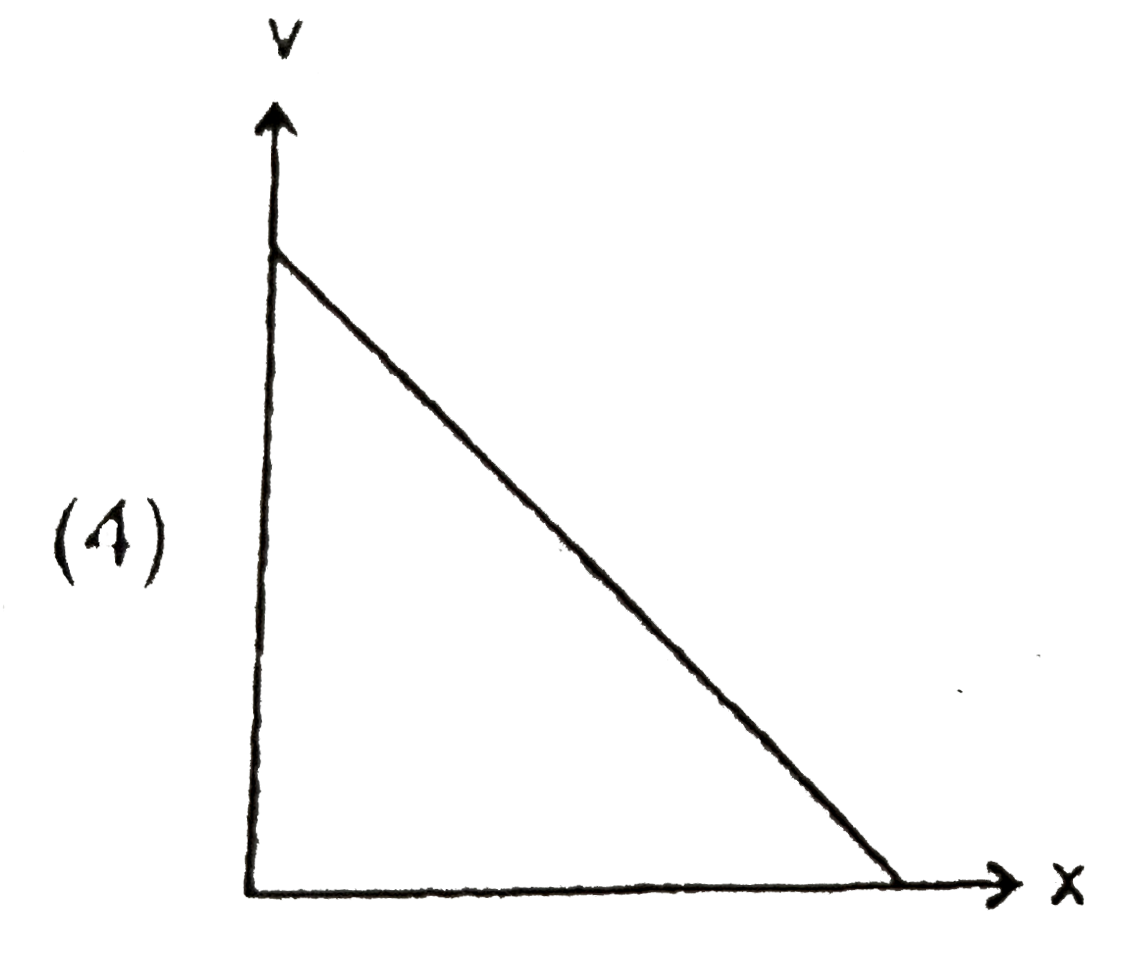
The correct Answer is:C
A body which ………..
a=g(sinθ−kxcosθ)
θ=cons.
v=g(sinθx−kx22cosθ)

Hence required graph will be as
Similar Questions
A body is moving down a long inclined plane of angle of inclination 'θ' for which the coefficient of friction varies with distance x as μ(x) = kx , where k is a constant . Here x is the distance moved by the body down the plane . The net force on the body will be zero at a distance x0 is given by ..........
View SolutionA body is moving down along inclined plane of angle of inclination theta The coefficient of friction between the body and the plane varies as mu=0.5x where x is the distance moved down the plane. The body will have the maximum velocity when
View Solution
Knowledge Check
- Question 1 - Select One
A body is moving down a long inclined plane of inclination 45∘ with horizontal. The coefficient of friciton between the body and the plane varies as μ=x/2, where x is the distance moved down the plane. Initially x=0&v=0
AWhen x=2 the velocity of the body is √g√2m/sBThe velocity of the body increases all the timeCAt an instant when v≠0 the instantaneous acceleration of the body down the plane is g(2−x)2√2DThe body first accelerates and then, decelerates. - Question 2 - Select One
A body is moving down a long inclined plane of angle of inclination θ. The coefficient of friction between the body and the plane varies as μ−0.1x, where x is the distance moved down the plane. The body will have the maximum velocity when it has travelled a distance x given by :
Ax=10tanθBx=5tanθC√2cotθDx=√10cotθ - Question 3 - Select One or More
A body is moving down a long inclined plane in inclination 45∘ with horizontal. The coefficient of friction between the body and the plane varies as μ=x/2, where x is the distance moved down the plane. Initially
x=0&v=0.AWhen x=2 the velocity of the body is √g√2m/sBThe velocity of the body increases all the timeCAt an instant when v≠0 the instantaneous acceleration of the body down the plane is
g(2−x)2√2DThe body first accelerates and then decelerates
A block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.
 View Solution
View SolutionA body of mass m slides down a rough plane of inclination α . If μ is the coefficient of friction, then acceleration of the body will be
View SolutionWhen a body of mass M slides down an inclined plane of inclination θ, having coefficient of friction μ through a distance s, the work done against friction is :
View SolutionA small mass slides down an inclined plane of inclination θ the horizontal the coefficient of friction is m=μ0x, where x is the distance by the mass before it stops is .
View SolutionA body of mass m slides down a rough plane of inclination α . If μ is the coefficient of friction, then acceleration of the body will be
View Solution

