The direction of motion of a projectile at a certain instant is inclined at an angle 60∘ to the horizontal. After √3 seconds it is inclined an angle 30∘. If the horizontal compound of velocity of projection is 3n (in m/sec) then value of n is : (takeg=10m/s2)
The correct Answer is:5
The direction ………………

Now ax=0
∴ucosα=vcosβ. ………. (1)
Now for motion along y axis
ay=−g
∴usinα−gt=vsinβ ………. (2)
V=Ucosαcosβin
we have.
usinα−gt=ucosαcosβsd∈β
or usinα−ucosαtanβ=gt
u{sinα−cosαtanβ}=gt
u=gt(sinα−cosαtanβ)
horizontal component of velocity =ucosα.
=gtcosα(sinα−cosαtanβ)=gt(tanα−tanβ)
=10×√3(√3−1√3)=15m/sec.
Similar Questions
The direction of a projectile at a certain instant is inclined at an angle ∝ to the horizontal , after t second, it is inclined at an angle β. Prove that the horizontal component of the velocity of the projectile is gttan∝−tanβ.
View SolutionTwo second after projection, a projectile is travelling in a direction inclined at 30∘ to the horizontal. After one more second, it is travelling horizontally. Find the magnitude and direction of the velocity of projection.
View Solution
Knowledge Check
- Question 1 - Select One
Two second after projection, a projectile is travelling in a direction inclined at 30∘ to the horizontal. After one more second, it is travelling horizontally. Find the magnitude and direction of the velocity of projection.
Athe velocity of projection is 20 m/sBthe velocity of projection is 20√3m/sCthe angle of projection is 30∘ with vertical.Dthe angle of projection is 30∘ with horizontal - Question 2 - Select One
A projectile is projected at 10ms−1 by making an angle 60∘ to the horizontal. After sometime, its velocity makes an angle of 30∘ to the horzontal . Its speed at this instant is:
A10√3B10√3C5√3D5√3 - Question 3 - Select One
A particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
A2.5 sB1.83 sC2.37 sD3.72 m
Two seconds after projection, a projectile is travelling in a direction inclined at 30∘ to the horizontal. After one more second, it is travelling horizontally. Find the magnitude and direction of its velocity.
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View SolutionA particle is thrown at time t=0 with a velocity of 10 m/s at an angle of 60∘ with the horizontal from a point on an incline plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is :
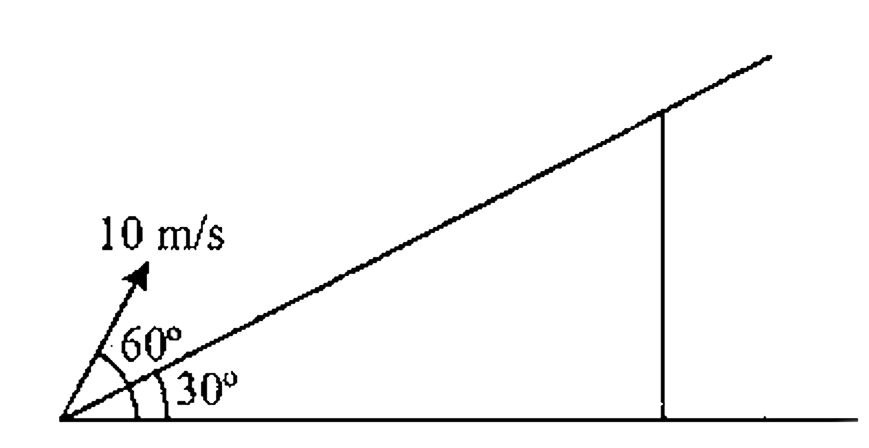 View Solution
View SolutionA particle is projected with the speed of 10√5m/sec. at an angle of 60∘ from the horizontal. The velocity of the projectile when it reaches the height of 10 m is (g=9.8m/sec2)
View Solution

