Force acting on a pasrticle is →F=(αyˆi+βxyˆj). Find the work done by this force, when pasrticle is moved alolng the line 2x=3y from origin to the point (3,2) {take quantities in SI units and α=1,β=1}
The correct Answer is:7
Force acting ………..
W=∫→F.d→r
=∫(ydx+xydy)
∵2x=3y
=∫20(32ydy+32y2dy)
∴Dx=32dy
=[34y2+y32]20=7 Joule.
Similar Questions
A force F=α+βx acts on a particle of mass m along the X . Axis . Here αandβ are constants . Find the work done by this force when particle moves form x = 0 to x = d .
View SolutionA force →F=xˆi+y2ˆjN acts on a particle and the particle moves from (1,2)m to (–3,4)m. Find work done by the force →F.
View Solution
Knowledge Check
- Question 1 - Select One
A force of →F=2xˆi+2ˆj+3z2ˆkN is acting on a particle. Find the work done by this force in displacing the body from (1,2,3)m to (3,6,1)m.
A(a) −10JB(b) 100JC(c) 10JD(d) 1J - Question 2 - Select One
A force →F=2xˆi+2ˆj+3z2ˆkN is acting on a particle .Find the work done by this force in displacing the body from (1,2,3)m to (3,6,1)m
A−10JB100JC10JD1J - Question 3 - Select One
A force →F=(3xy−5z)ˆj+4zˆk is applied on a particle. The work done by the force when the particle moves from point (0,0,0) to point (2,4,0) as shown in figure.
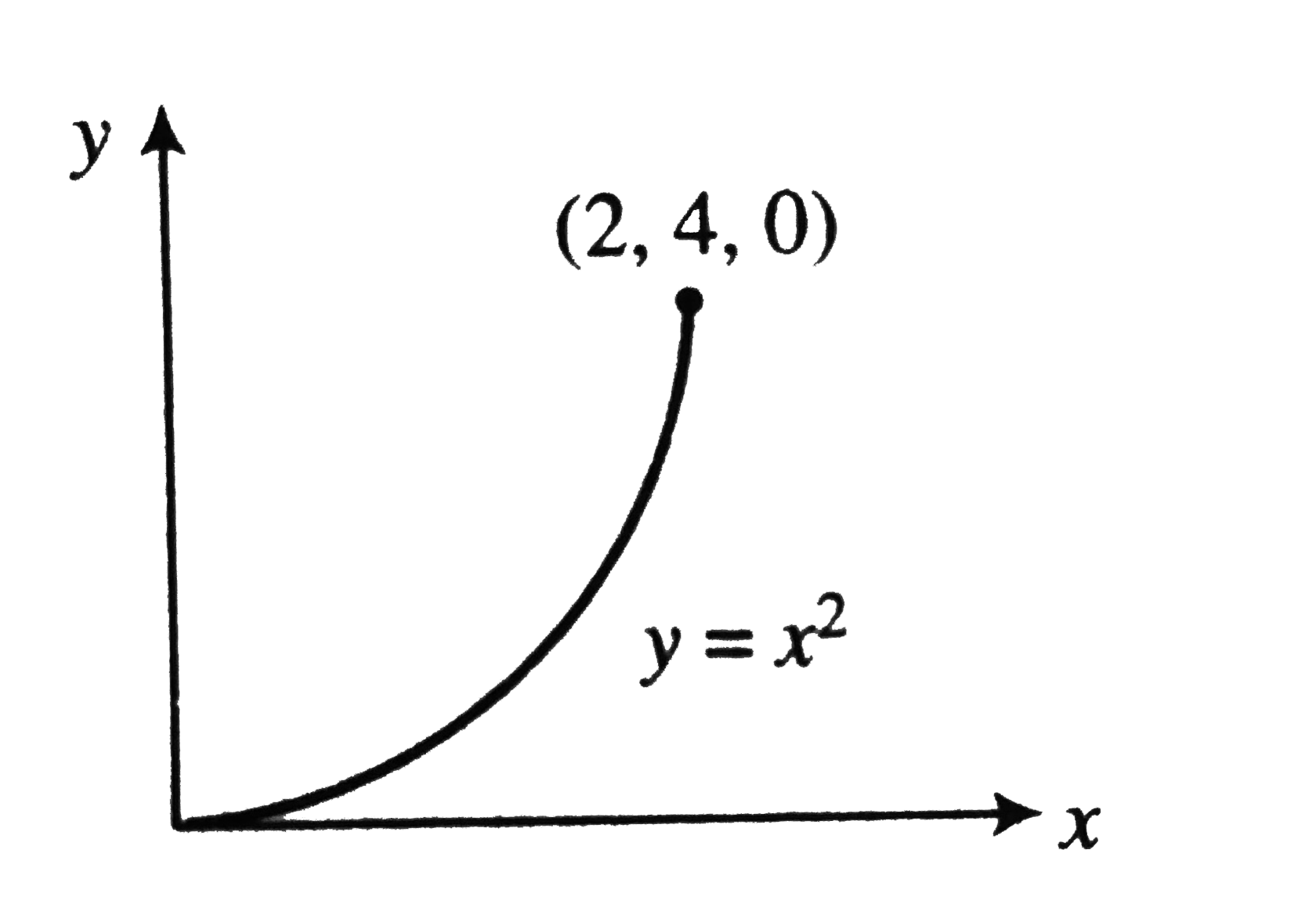 A(a) 2805unitsB(b) 1405unitsC(c) 2325unitsD(d) 1925units
A(a) 2805unitsB(b) 1405unitsC(c) 2325unitsD(d) 1925units
Find the moment of force →F=ˆi+ˆj+ˆk acting at point (−2,3,4) about the point (1,2,3).
View SolutionA force →F=2ˆi+ˆj−ˆk acts at point A whose position vector is2ˆi−ˆj. Find the moment of force →F about the origin.
View SolutionConsider a force →F=−xˆi+yˆj. The particle is moved from point A(1,0) to B(0,1) along the line segment. The work done by force is (All quantities are in Si units)
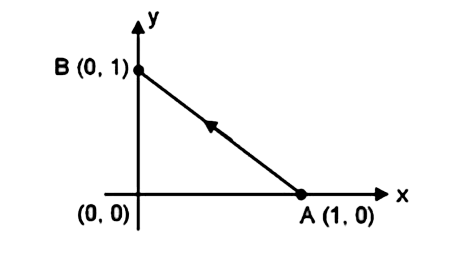 View Solution
View SolutionThe work done by the forces →F=2ˆi−ˆj−ˆk in moving an object along the vectors 3ˆi+2ˆj−5ˆk is:
View SolutionA force →F=6xˆi+2yˆj displaces a body from →r1=3ˆi+8ˆj to →r2=5ˆi−4ˆj. Find the work done by the force.
View Solution

