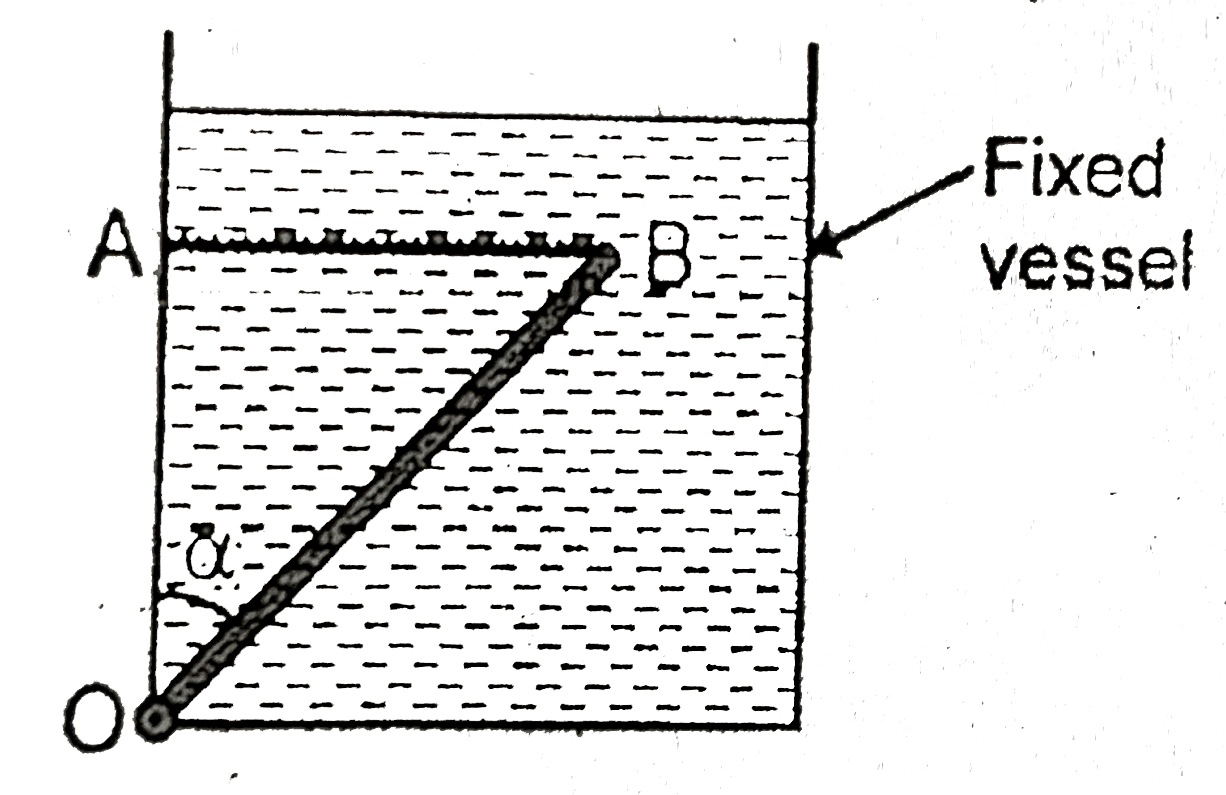
A uniform rod of length , cross-sectional areal and relative density is free to rotate about smooth hinge in vertical plane. The rod is held with a horizontal string which can withstand a maximum tension of . The rod and string system is kept in water as shown in figure. The maximum value of angle which the rod can make with vertical without breaking the string is
The correct Answer is:B
A uniform rod ………….
of rod :
Torque about :

(For equilibrium)
Similar Questions
One end of a uniform rod of mass M and length L is supproted by a frictionless hinge which can with stand a tension of 1.75Mg. The rod is free to rotate in a vertical plane. The maximum angle should the rod be rotated from the vertical position so that when left, the hinge does not brek is πn
View SolutionA thin rod MN free to rotation in the vertical plane about the fixed end N is held horizontal when the end M is released the speed of this end when the rod makes an angle α with the horizontal will be proportional to : (see figure)

View Solution
Knowledge Check
A uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
Amω2l23AYBmω3l33AYCmω2l34AYDmω3l23AYA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?A47B57mgC137mgD117mgA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
 Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
A uniform rod of mass m length l is attached to smooth hinge at end A and to a string at end B as shown in figure. It is at rest. The angular acceleration of the rod just after the string is cut is :

View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is

View Solution
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is
View SolutionConsider the situation shown in the figure. Uniform rod of length L can rotat freely about the hinge A in vertical plane. Pulleys and stringa are light and frictionless. If the rod remains horizontal at rest when the system is released then the mass of the rod is
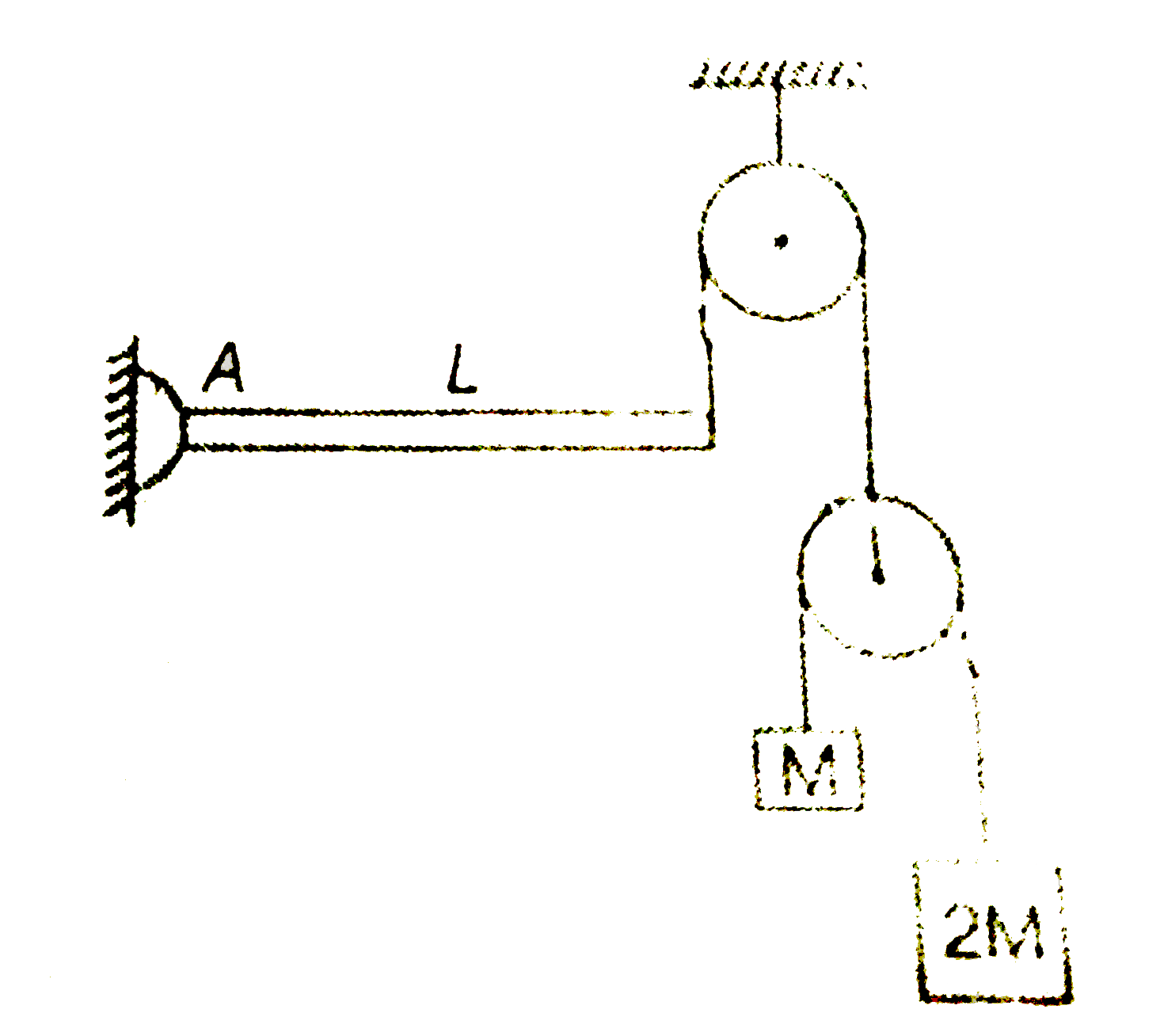
View Solution
