Equation of trajectory of a projectile is given by $y = - x^{2} + 10 x$ where $x$ and $y$ are in meters and $x$ is along horizontal and $y$ is vericall $y$ upward and particle is projeted from origin. Then : $(g = 10) m / s^{2}$

A

initial velocity of particle is $\sqrt{505} m / s$

B

horizontal range is $10 m$

C

maximum height is $25 m$

D

angle of projection with horizontal is ${tan}^{- 1} (5)$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

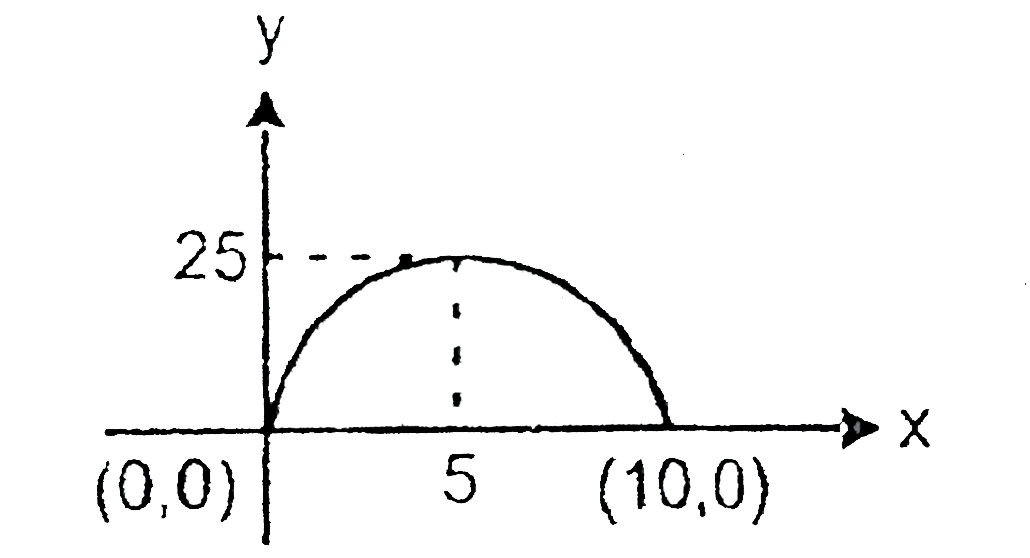
$R = 10 m$
$H = 25 m$
$\frac{u^{2} {sin}^{2} θ}{2 g} = 25 \Rightarrow u sin θ = 10 \sqrt{5}$
$\frac{d y}{d x}$ at $(0, 0)$
$t e n θ = 10$
$sin θ = \frac{10}{\sqrt{101}}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The equation of trajectory of a projectile is given by $y = 4 x - \frac{40}{39} x^{2}$ , where y is verticaly upwards. If R is range and $θ$ is angle of projection from horizontal, then value of $R tan θ$ is (x and y are inm)
A3.9m
B15.6m
C11.7m
D14.2
Question 2 - Select One
The trajectory of a projectile in a vertical plane is $y = a x - b x^{2}$ , where $a and b$ are constant and $x and y$ are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.
A $\frac{b^{2}}{2 a}, {tan}^{- 1} (b)$
B $\frac{a^{2}}{b}, {tan}^{- 1} (2 b)$
C $\frac{a^{2}}{4 b}, {tan}^{- 1} (a)$
D $\frac{2 a^{2}}{b}, {tan}^{- 1} (a)$
Question 3 - Select One
The equation of trajectory of an oblique projectile $y = \sqrt{3} x - \frac{g x^{2}}{2}$ . The angle of projection is
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $15^{\circ}$

RESONANCE-TEST PAPERS-FST-3

Home
Ask Doubt
Profile