On a disc of radius R a concentric circle of radius R/2 is drawn. The disc is free to rotate about a frictionless fixed axis through its center and perpendicular to plane of the disc. All three forces ( in plane of the disc ) shown in figure are exerted tangent to their respective circular periphery. The magnitude of the net torque ( about centre of disc ) acting on the disc is :
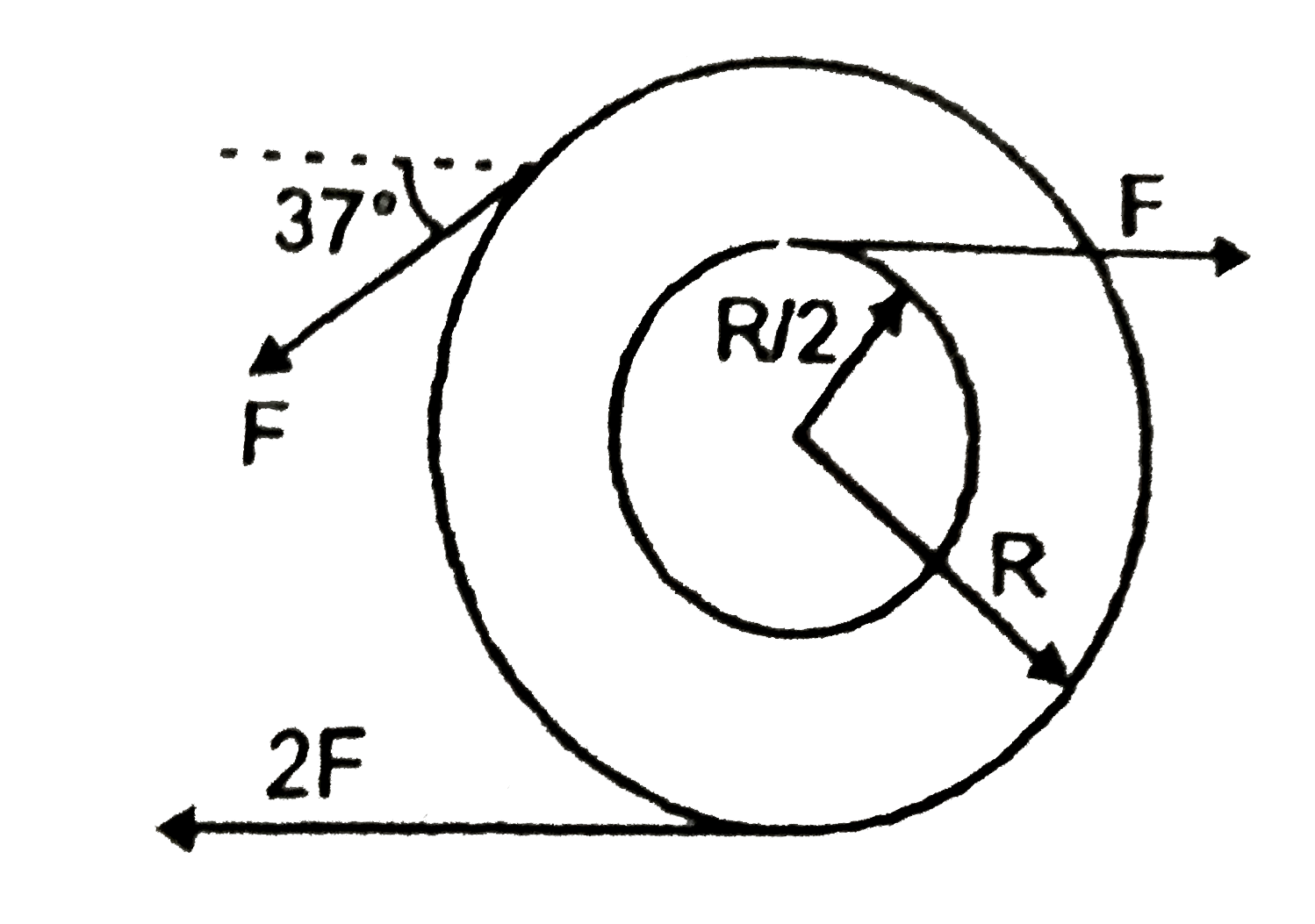
1.5FR
1.9FR
2.3FR
2.5FR
The correct Answer is:A
Toreque τ=(2f)R+F(R2)+FR(−1)=3FR2
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Physics
775 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 2
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS
127 Videos
Similar Questions
A disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionA circular hole of radius r/2 is cut from a circular disc of radius 'r'. The disc lies in the xy plane. Determine the moment of inertia about an axis passing through the centre and perpendicular to the plane of the disc.
View Solution
Knowledge Check
Radius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
AR/√2BR/2C√2 RD2RA metallic circular disc having a circular hole at its centre rotates about an axis passing through its centre and perpendicular to its plane. When the disc is heated:
Aits angular speed will decreaseBits diameter will decreaseCits moment of inertia will increaseDits angular speed will increaseA metallic circular disc having a circular hole at its centre rotates about an axis passing through its centre and perpendicular to its plane. When the disc is heated:
Aits speed will decreaseBits diameter will decreaseCits moment of inertial will increaseDits speed will increase
A disc of mass 2 kg and diameter 40 cm is free to rotate about an axis passing through its centre and perpendicular to its plane. If a force of 50 N is applied to the disc tangentially Its angular acceleration will be
View SolutionA metallic circular disc having a circular hole at its centre rotates about an axis passing through its centre and perpendicular to its plane. When the disc is heated, choose the wrong statement
View SolutionThe moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
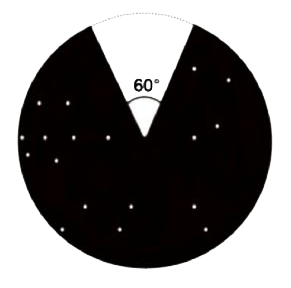
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionA disc of mass 4 kg and radius 0.2 m, makes 20 rev/s, about an axis passing through its centre and perpendicular to the plane of the disc. The angular momentum of the disc is approximately equal to
View Solution
