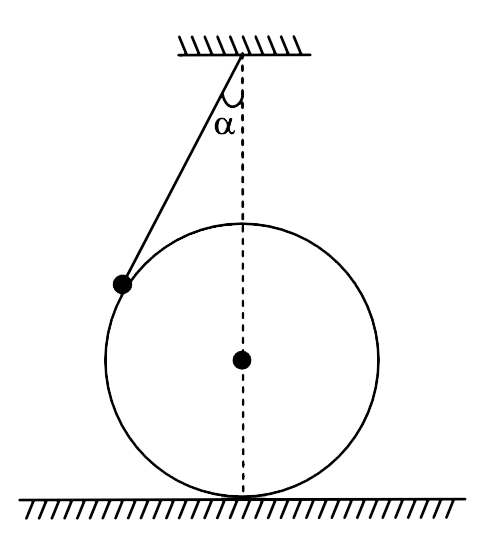
A sphere of mass M is held at rest on a horizontal floor. One end of a light string is fixed at a point that is vertically above the centre of the sphere. The other end of the string is connected to a small particle of mass m that rest one the sphere. The string makes an angle α=30∘ with the vertical. Then the acceleration of the spherer immediately after it is released is : (There is no frication anywhere and string is tangene to the sphere) :

√3mg3m+2M
√3mg2m+4M
√2mg3m+4M
√3mg3m+4M
The correct Answer is:D
Since the particle is small, the string will be trangential to the sphere.θ=60∘ (see figure).
Let acceleration of the sphere be a0 immediately after release
The particle will have its initial acceleration (a) along normal to the string towards PC. And, component of a0 in the direction →PC must be equal to a

∴a=a0cos(90−θ)=a0sinθ=√32a0
Force on the particle has been shown in figure. The equation of motion along PC will be
mgcosθ−N=ma⇒12mg−N=√32ma0 .......(i)
Sphere experiences a forces N along PC. It has a horizontal component =Nsinθ.......(ii)
From (i) and (ii)12mg=(√3m2+2M√3)a0
a0=√3mg3m+4M
Similar Questions
A sphere of mass M is held at rest on a horizontal floor. One end of a light string is fixed at a point that is vertically above the centre of the sphere. The other end of the string is connected to a small particle of mass m that rests on the sphere. The string makes an angle α=30∘ with the vertical. Find the acceleration of the sphere immediately after it is released. There is no friction anywhere.
 View Solution
View SolutionA small body tied to one end of the string is whirled in a vertical circle. Represent the forces on a diagram when the string makes an angle θ with initial position.
View Solution
Knowledge Check
- Question 1 - Select One
A bob of mass m=50g is suspended form the ceiling of a trolley by a light inextensible string. If the trolley accelerates horizontally, the string makes an angle tˆa=37∘ with the vertical. Find the acceleration of the trolley.
 A10m/s2B12.5m/s2C7.5m/s2D7.5m/s
A10m/s2B12.5m/s2C7.5m/s2D7.5m/s - Question 2 - Select One
A block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
Am2gm1+m2Bm1gm1+m2CgDm2gm1 - Question 3 - Select One
A pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
AmgsinθBmgCqEsinθDqEcosθ
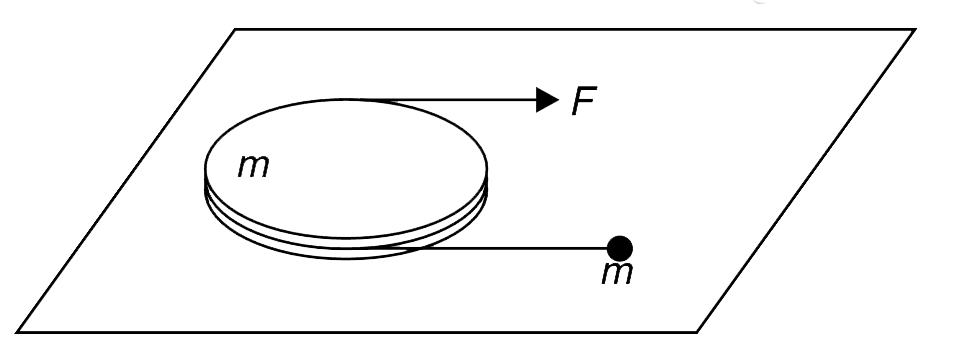
A disc of mass m lies flat on a smooth horizontal table. A light string runs halfway around it as shown in figure. One end of the string is attached to a particle of mass m and the other end is being pulled with a force F. There is no friction between the disc and the string. Find acceleration of the end of the string to which force is being applied.
 View Solution
View SolutionA hemisphere of mass M and radius R rests on a smooth horizontal table. A vertical rod of mass m is held between two smooth guide walls supported on the sphere as shown. There is no friction between the rod and the sphere. A horizontal string tied to the sphere keeps the system at rest.
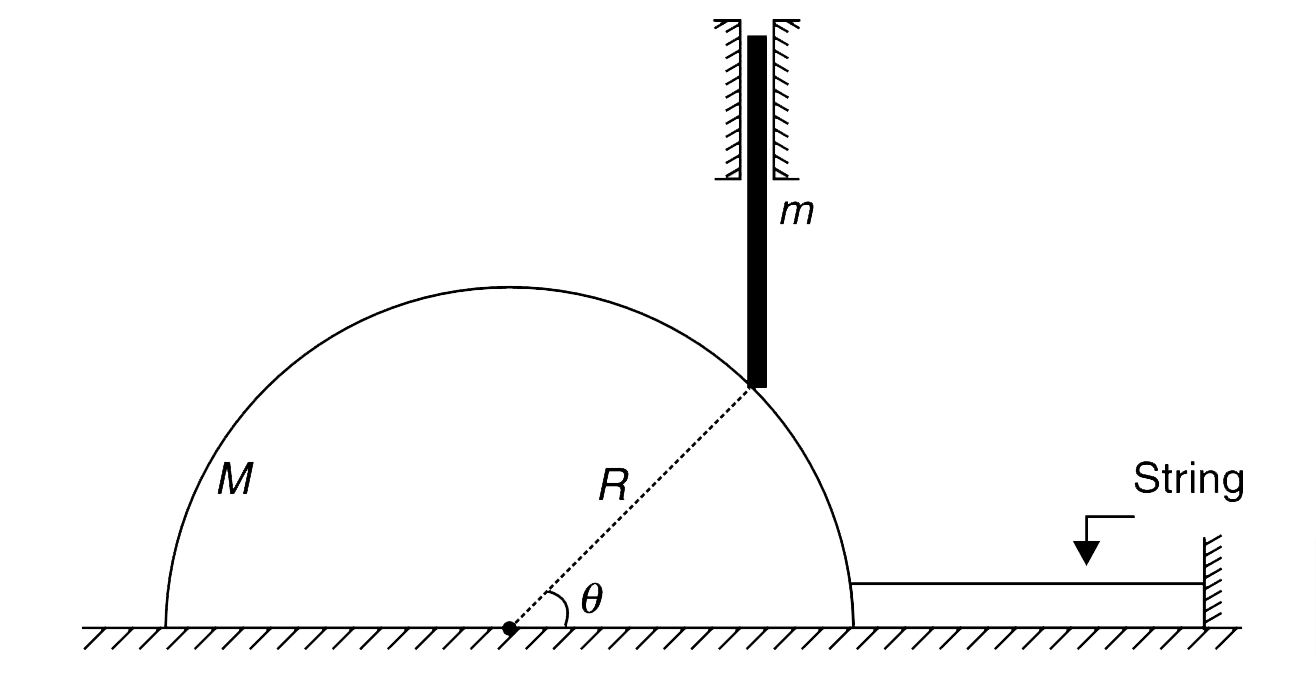
(a) Find tension in the string.
(b) Find the acceleration of the hemisphere immediately after the string is cut.View SolutionA body of mass m hangs at one end of a string of length l , the other end of which is fixed. It is given a horizontal velocity so that the string would just reach where it makes an angle of 60∘ with the vertical. The tension in the string at mean position is
View SolutionA body of mass m hangs at one end of a string of length l, the other and of which is fixed . It is given a horizontal velocity so that the string would just reach where it makes an angle of 30∘ with the vertical . The tension in the string at mean position is
View SolutionA body of mass m hangs at one end of a string of lenth l, the other end of which is fixed. It is given a horizontal velocity so that the string would just reach where it makes an angle of 60∘ with the vertical. The tension in the string at bottommost point position is
View Solution

