There is a step of height h on an incline plane. The step prevents a ball of radius R from rolling down. If the inclination (θ) to the incline is increased gradualluy, at some value of θ the ball will just manage to climb the step then value of θ is.
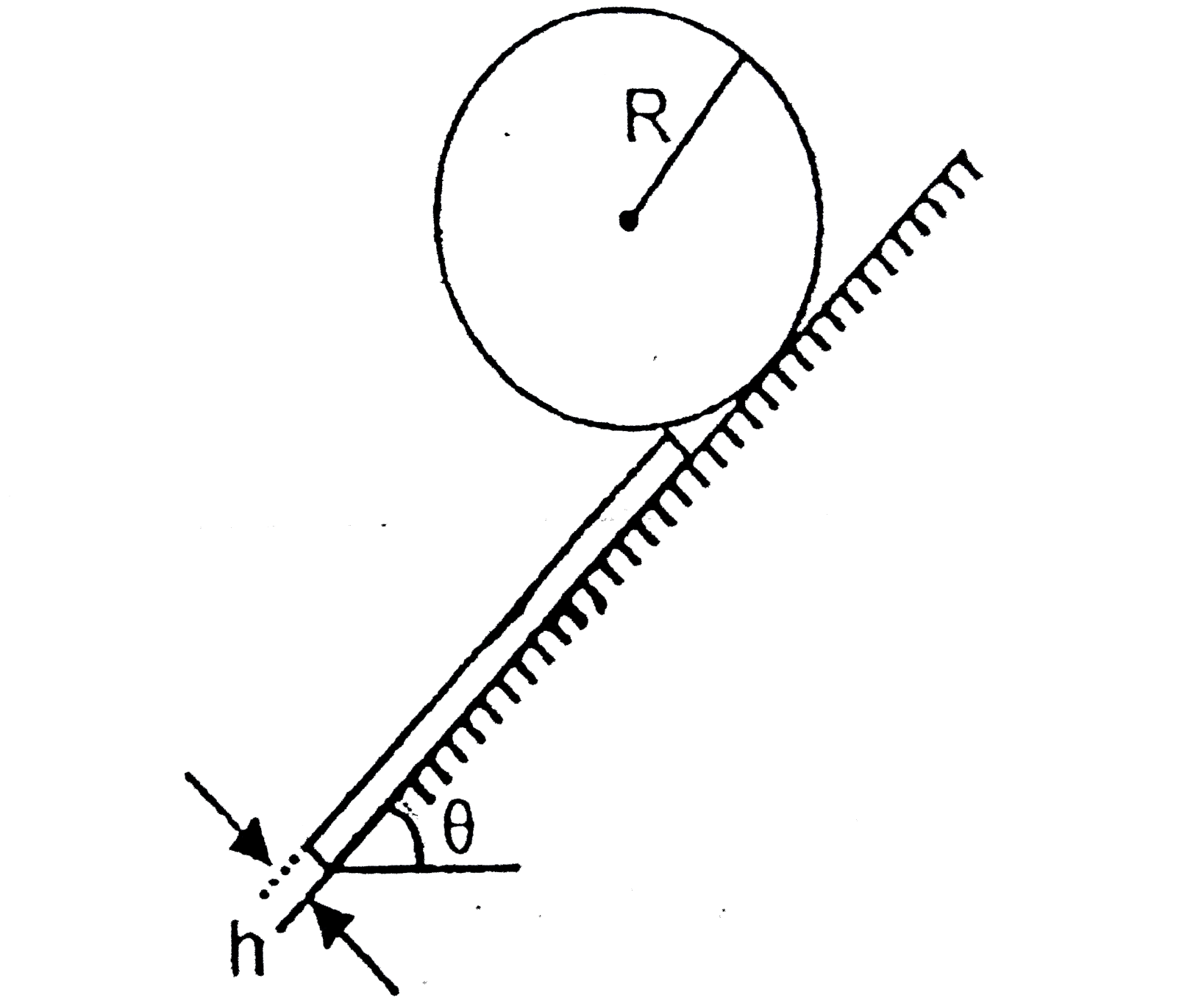
cosθ=RR+h
cosθ=R−hR
cosθ=R−2hR
sinθ=R−hR
The correct Answer is:B
(a) The ball begin to climb the step if the line of action of its weight (Mg) passes to the left to point A. This will cause an unbalanced torque about A.
In critical case (see figure) cosθ=R−hR
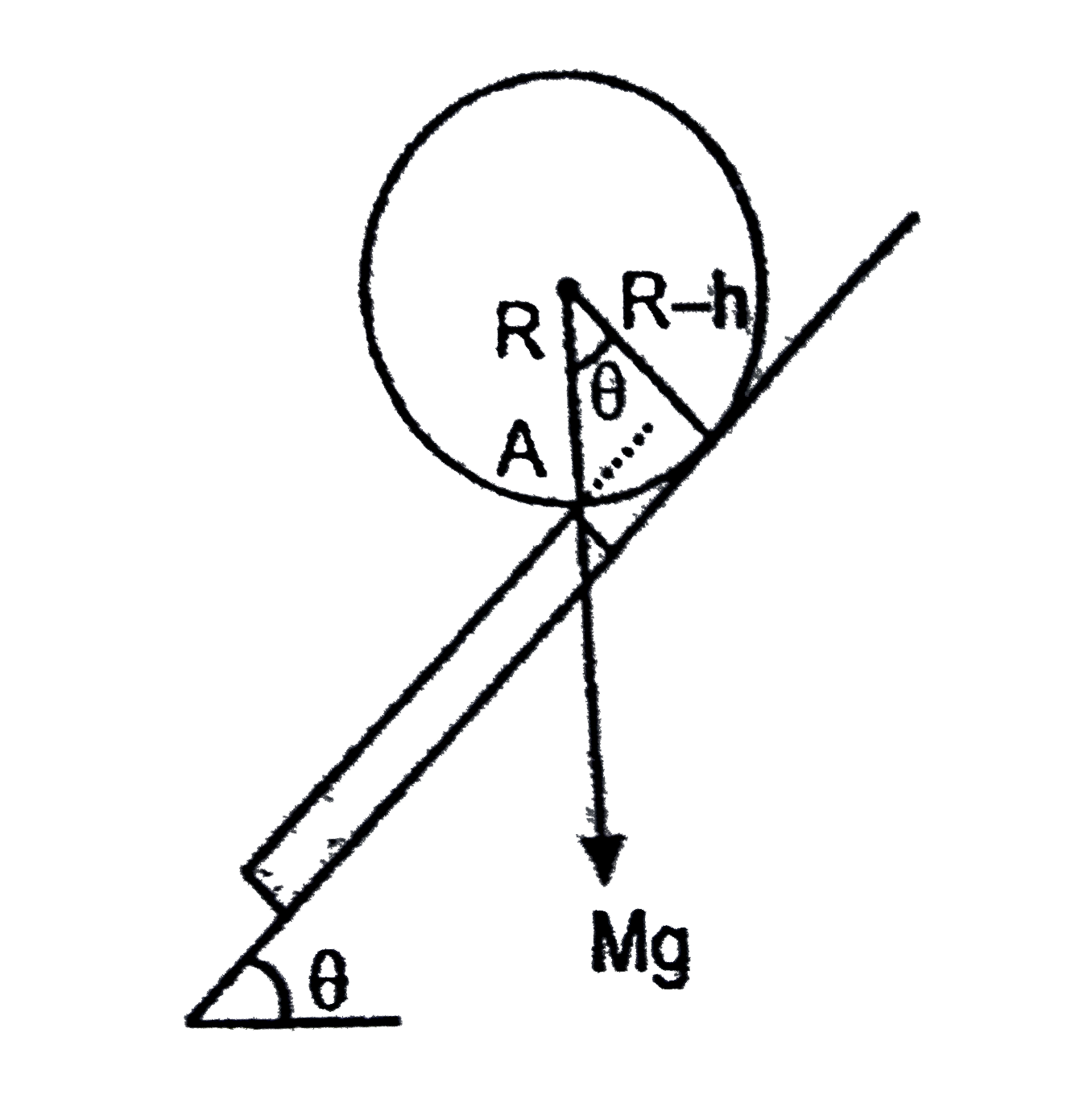
(b) In the position shown, the COM of the ball is vertically above point A at a distance R. As the ball climbs, its centre of mass will lover from this position. (Otherwise why will the ball come down?) In the position shown the centre of mass is at highest position.
Similar Questions
There is a step of height h on an incline plane. The step prevents a ball of radius R from rolling down.
(a) If the inclination (θ) of the incline is increased gradually, at what value of θ the ball will just manage to climb the step?

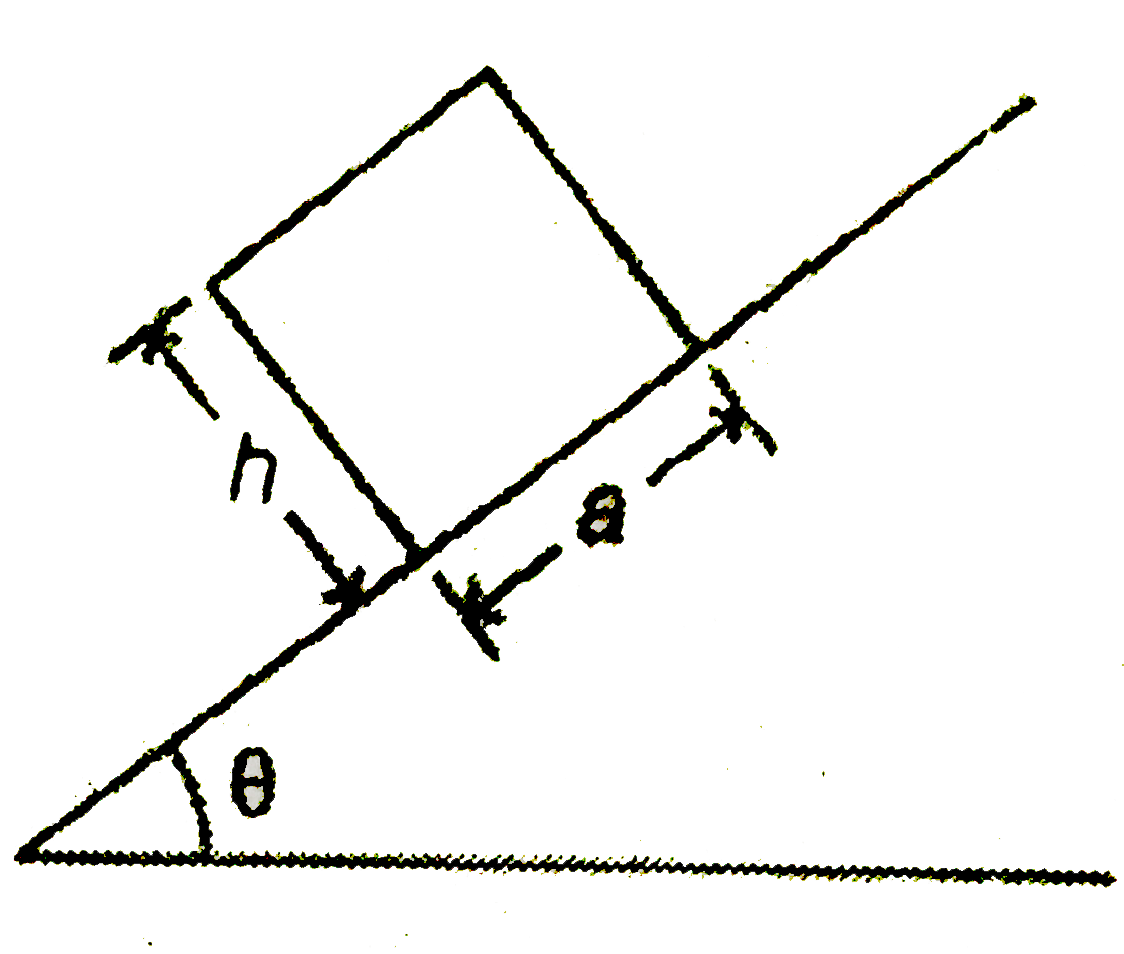
(b) Does the gravitational potential energy of the ball increases or decreases as it climbs the step ?View SolutionA block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A spherical shell of radius R is rolling down an incline of inclination θ without slipping. Find minimum value of coefficient of friction.
 A27tanθB25tanθC23tanθDNone
A27tanθB25tanθC23tanθDNone - Question 2 - Select One
The acceleration down the plane of spherical body of mass m radius R and moment of inertia I having inclination θ to the horizontal is
Agsinθ1+12/R2Bgsinθ1+I/R2Cgsinθ1+I/MR2DgsinθMR2+1 - Question 3 - Select One
A disc of radius R is rolling down an inclined plane whose angle of inclination is θ Its acceleration would be
A57gsinθB23gsinθC12gsinθD35gsinθ
A sphere is rolling down a plane of inclination θ to the horizontal. The acceleration of its centre down the plane is
View SolutionA solid cylinder is rolling down a rough inclined plane of inclination θ. Then
View SolutionA block with a square base measuring axa and height h, is placed on an inclined place. The coefficient of friction is m. The angle of inclination (θ) of the plane is gradually increased. The block will.
View SolutionThe force required to just move a body up an inclined plane is double the force the required prevent it from sliding down. If phi is angle of friction and theta is the angle which incline makes with the horizontal then,
View SolutionTwo balls are thrown from an inclined plane at angle of projection with the plane, one up the incline and the other down the incline as shown. Which one is not correct?
 View Solution
View Solution

