A nonconducting cylinder having volume 2V0 is partitioned by a fixed non conducting wall in two equal part. Partition is attached with a valve. Right side of the partition is a vacuum and left part is filled with a gas having pressure and temperature P0 and T0 respectively. If valve is opened find the final pressure and temperature of the two parts.
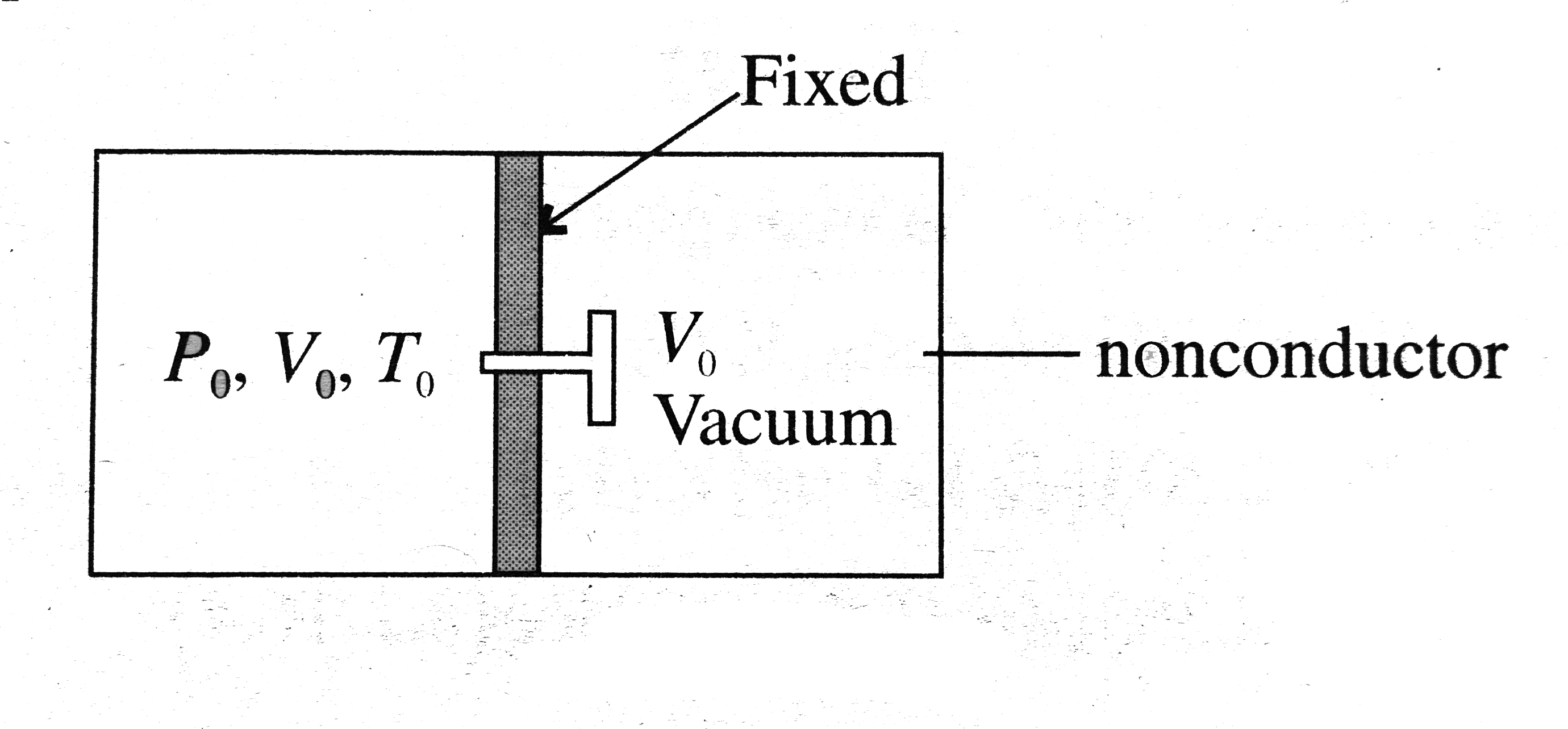
From the first law thermodynamics ΔQ=ΔU+W
Since gas expands freely therefore w=0, since no heat is given to gas ΔQ=0
⇒ΔU=0 and temperature remains constant.
Tfinal=T0
Since the process is isothermal therefore P0×V0=Pfinal×2V0⇒Pfinal=P0/2
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - KTG & THERMODYNAMICSEXERCISE - Solved problem1videos
KTG & THERMODYNAMICS
- BOOK - RESONANCECHAPTER - KTG & THERMODYNAMICSEXERCISE - Problem3videos
KTG & THERMODYNAMICS
- BOOK - RESONANCECHAPTER - KTG & THERMODYNAMICSEXERCISE - SUBJECTIVE QUESTIONS27videos
KTG & THERMODYNAMICS
- BOOK - RESONANCECHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise64videos
KINETIC THEORY OF GASES AND THERMODYNAMICS
- BOOK - RESONANCECHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise65videos
MAGNETIC FIELD AND FORCES
Similar Questions
A monoatomic gas is enclosed in a nonconducting cylinder having a piston which can move freely. Suddenly gas is compressed to 1/8 of its initial volume. Find the final pressure and temperature if initial pressure and temperature are P0 and T0 respectively.
 View Solution
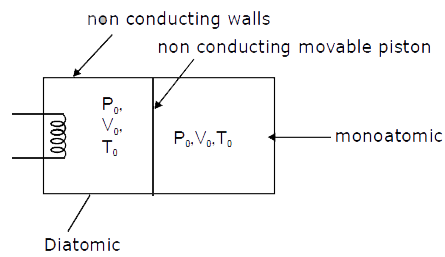
View SolutionA cylindrical container having nonconducting walls is partitioned in two equal parts such that the volume of the each parts is equal toV0. A movable nonconducting piston is kept between the two parts. Gas on left is slowly heated so that the gas on right is compressed upto volume V08. Find pressure and temperature on both sides if initial pressure and temperature, were P0andT0 respectively. Also find heat given by the heater to the gas. (number of moles in each part is n)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A container with insulating walls is divided into two equal parts by a partition fitted with a valve. One part is filled with an ideal gas at a pressure P and temperature T, whereas the other part is completely evacuated . If the valve is suddenly opened, the pressure and temperature of the gas will be
AP2,TBP2,T2CP, TDP,T2 - Question 2 - Select One
Ten moles of a diatomic perfect gas are allowed to expand at constant pressure. The initial volume and temperature are V0 and T0 respectively. If 72RT0 heat is transferred to the gas, then the final volume and temperature are
A(a) 1.1V0,1.1T0B(b) 0.9V0,0.9T0C(c) 1.1V0,1011T0D(d) 0.9V0,109T0 - Question 3 - Select One
Two thermally insulated vessel 1 and 2 are filled with air at temperature (T1T2),volume(V1V2) and pressure (P1P2) respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
AT1T2(P1V1+P2V2)/(P1V1T2+P2V2T1)B(T1+T2)/2CT1+T2DT1T2(P1V1+P2V2)/(P1V1T1+P2V2T2)
In given figure, an adiabatic cylindrical tube of volume 2V0 is divided in two equal parts by a frictionless adiabatic separator. An ideal gas in left side of a tube having pressure P1 and temperature T1 where as in the right side having pressure P2 and temperature T2.Cp/Cv=γ is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the final volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases,
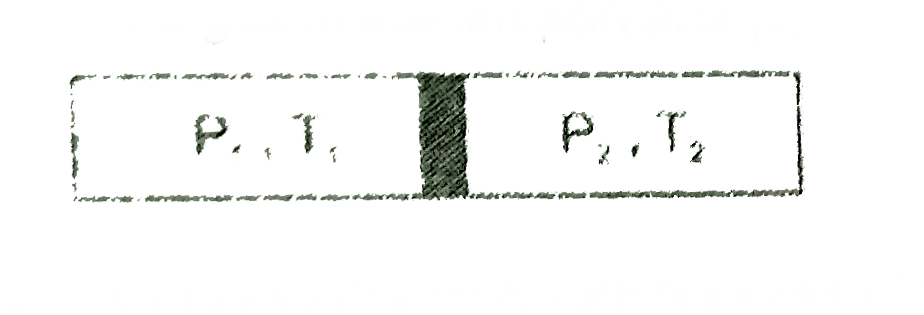 View Solution
View SolutionA thermally insulated container is divided into two parts by a screen. In one part the pressure and temperature are P and T for an ideal gas filled. In the second part it is vacuum. If now a small hole is created in the screen, then the temperature of the gas will
View SolutionA thermally insulated container is divided into two parts by a screen. In one part the pressure and temperature are P and T for an ideal gas filled. In the second part it is vacuum. If now a small hole is created in the screen, then the temperature of the gas will
View SolutionA cylindrical adiabatic container of total volume 2V0 divided into two equal parts by a conducting piston which is free to move as shown in figure. Each part containing identical gas at pressure P0. Initially temperature of left and right part is 4T0andT0 respectively. An external force is applied on the piston of area 'A' to keep the piston at rest. The value of external force required when thermal equilibrium is reached is.
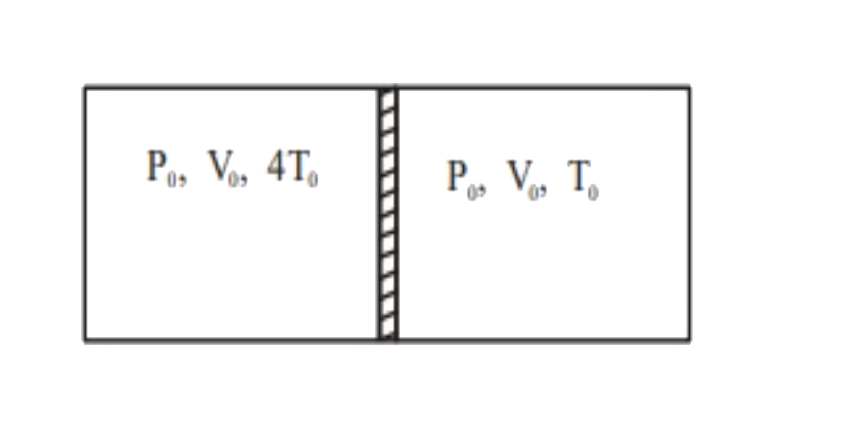 View Solution
View SolutionTwo gases A and B having the same pressure P, volume V and temperature T are mixed. If mixture has volume and temperature as V and T respectively, then the pressure of the mixture will be
View Solution

