If ideal diatomic gas follows the process, as shown in graph, where $T$ is temperature in kelvin and $V$ is volume $(m^{3})$ , then molar heat capacity for this process will be [in terms of gas constant $R]$ :

A

$\frac{7 R}{2}$

B

$5 R$

C

$\frac{19 R}{6}$

D

$\frac{11 R}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$C = C v + \frac{R}{1 - η} \dots \dots . . (i)$
$T^{2} V^{- 3} =$ constant $, P V = n R T$
$P^{2} V^{2} V^{- 3} =$ constat $, P^{2} V^{- 1} =$ constant
$P V^{- 1 / 2} =$ constant
$N = - 1 / 2$
$C = \frac{5 R}{2} + \frac{2 R}{3} = \frac{19 R}{6}$

|

Updated on:21/07/2023

Class 11 PHYSICS THERMODYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The molar heat capacity of a gas in a process
Ais either $C_{V} or C_{P}$
Blies between $C_{V} or C_{P}$
Cmay range from zero to infinity
Dcan have any real value
Question 2 - Select One
The pressure P of an ideal diatomic gas varies with its absolute temperature T as shown in figure. The molar heat capacity of gas during this process is [R is gas constant]

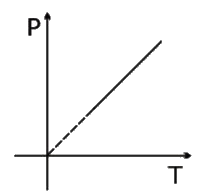A1.7 R
B3.25 R
C2.5 R
D4.2 R
Question 3 - Select One
One mole of diatomic ideal gas undergoing a process in which absolute temperature is directely proportional to cube of volume, then, heat capacity of process is :
A $\frac{10}{3} R$
B $\frac{11}{6} R$
C $\frac{17}{6} R$
D3R

RESONANCE-KTG & THERMODYNAMICS-PART -I

Home
Ask Doubt
Profile