Consider the situation shown in figure. The frame is made of the same material and has a uniform cross-sectional area everwhere. If amount of heat flowing per second through a cross-section of part A is 60J. The amount of total heat taken out per second from the end at 50∘C is 0.132×10nJ/s. Find 'n'.
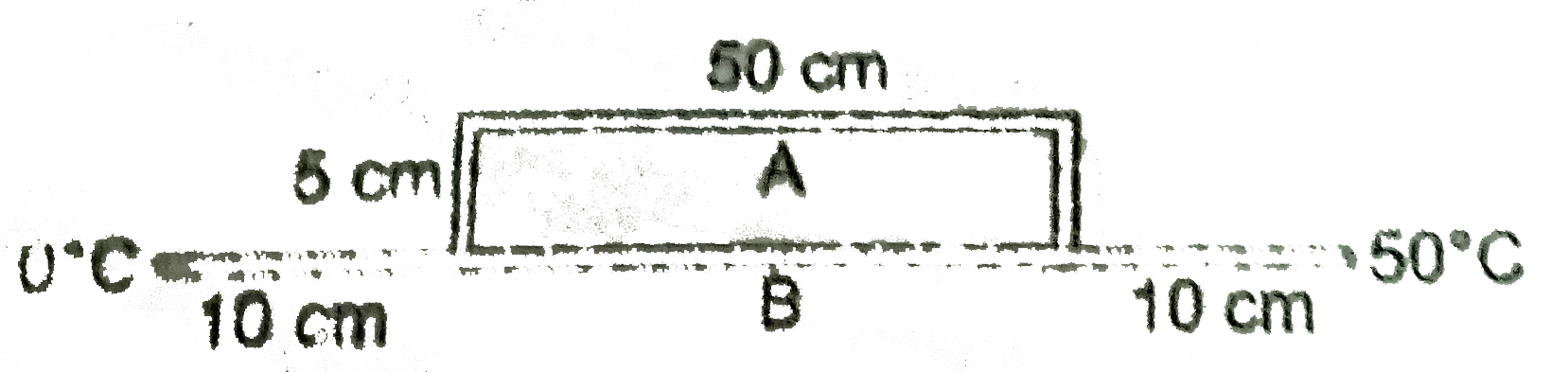
The correct Answer is:3

R1= thermal resistance of bent part
=60KA,R2=50KA
(R2R1+R2)Q=60J/s⇒Q=132J/s
Topper's Solved these Questions
- HEAT TRANSFERBook:RESONANCEChapter:HEAT TRANSFERExercise:Exercise-3
Explore 1 Video
- HEAT TRANSFERBook:RESONANCEChapter:HEAT TRANSFERExercise:Advancel Level Problems
Explore 17 Videos
- HEAT TRANSFERBook:RESONANCEChapter:HEAT TRANSFERExercise:Exercise-2
Explore 1 Video
- GRAVITATIONBook:RESONANCEChapter:GRAVITATIONExercise:Exercise
Explore 21 Videos
- KINEMATICSBook:RESONANCEChapter:KINEMATICSExercise:Exercise
Explore 65 Videos
Similar Questions
Conside the situation shown in figure. The frame is made of the same material and has a unifrom cross-section area everywhere. Calculate the amount of heat flowing per second through a cross section of the bent part if the total heat taken out per second from the end at 100∘C is 130J .
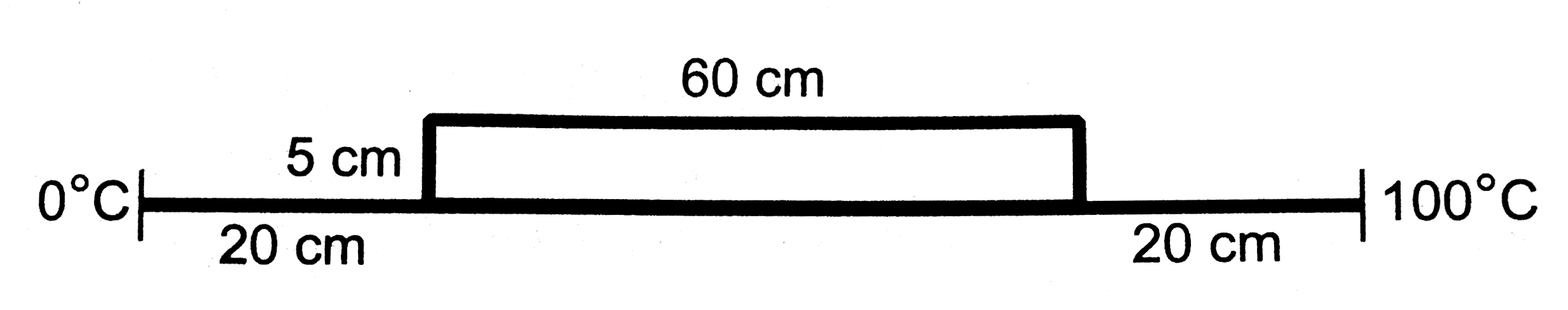
View SolutionA semicircular rods is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod formss a diameter of the other rod. The junction are maintaine dat different temperature. Find the ratio of the heat transffered through a cross section of the straigh rod in a given time.
View Solution
Knowledge Check
Three rods are made from the same material and having the same cross-sectional area and length have been joined as shown in the figure.
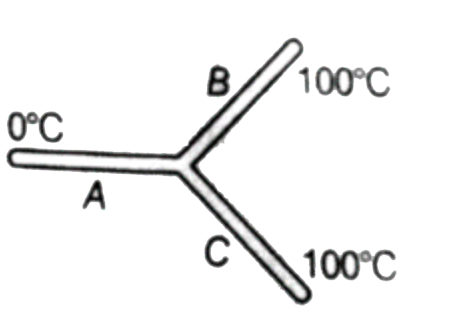
The left end and right end are kept 0∘Cand100∘C , respectively . The temperature of the junction of three rods will beA50∘CB60∘CC80∘CD66.66∘CTwo rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.
 A2πB1πCπDπ2
A2πB1πCπDπ2The lengths and radii of two rods made of same material are in the ratios 1 : 2 and 2 : 3 respectively. If the temperature difference between the ends for the two rods be the same, then in the steady state, the amount of heat flowing per second through them will be in the ratio
A1:3B4:3C8:9D3:2
(a) Three rod of lengths 20cm each and area of cross-section 1cm2 are joined to form a triangle ABC. The conductivities of the rods are KAB=50J/m−s−.∘C,KBC=200J/m−s−.∘C and KAC=400J/m−s−.∘C. The junctions A,B and C are maintained at 40∘C, 80∘C and 80∘C respectively. Find the rate of heat flowing through the rods AB,AC and BC.
(b) A semicircular rod is joineted as its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross-section of the simicircular rod to the heat transferred through a cross-section of the straight rod in a given time.
View SolutionFigure shows a steel rod joined to a brass eod. Each of the rods has length of 31cm and area of cross-section 0.20cm2. The junction is maintained at a constant temperature 50∘C and the two ends are maintained at 100∘C. The amount of heat taken out from the cold junction in 10 minutes after the steady state is reached in n×102J. Find 'n' the thermal conductivities are Ksteel=46W/m−∘C and Kbrass=109W/m−∘C.

View SolutionThe ratio of cross-sectional areas of two conducting wires made up of same material and having same length is 1: 2. What will be the ratio of heat produced per second in the wires, when same current is flowing in them?
View SolutionTwo wires are made of the same material and have the same volume. However wire 1 has cross-sectional area A and wire 2 has cross-sectional area 3A. If the length of wire 1 increases by Δx on applying force F, how much force is needed to stretch wire 2 by the same amount?
View SolutionA conductor of length l and area of cross-section A has n number of electrons per unit volume of the conductor. The current flowing through conductor in time t is given by
View Solution