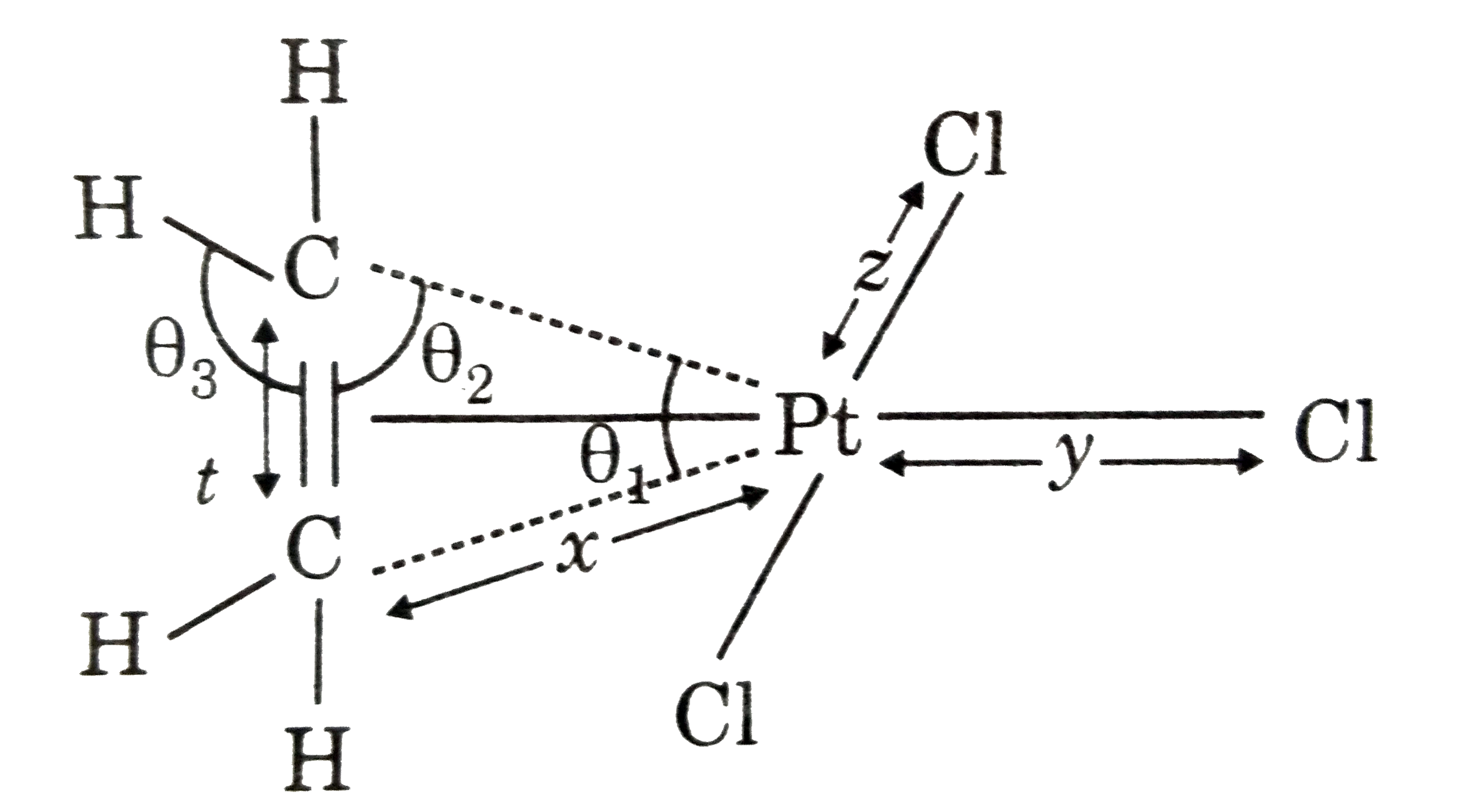
Here, $θ_{1}, θ_{2} and θ_{3}$ are bond angles, x, y, z, t are bond lengths in ZEISE'S Salt.
Write the number of correct relationships
$(a) y < z (b) x > z$
$(c) x > y (d) t < y$
$(e) θ_{1} < θ_{2} (f) θ_{3} > θ_{2}$
$(g) x = y = z (h) θ_{1} = θ_{2}$

Text Solution

Verified by Experts

The correct Answer is:3

$x = 2.13 Å, y = 2.33 Å, z = 2.30 Å, t = 1.37 Å, θ_{1} = 38^{\circ}, θ_{2} = 71^{\circ}, θ_{3} = 120^{\circ}$
Correct relationship (d),(e ),(f)

|

Updated on:21/07/2023

Class 12 CHEMISTRY COORDINATION COMPOUNDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $x = θ - \frac{1}{θ} and y = θ + \frac{1}{θ}, then: \frac{d^{2} y}{{d x}^{2}} =$
A $\frac{y}{x}$
B $\frac{x^{2} - y^{2}}{y^{3}}$
C $\frac{y^{2} - x^{2}}{x^{3}}$
D $\frac{y^{2} - x^{2}}{y^{3}}$
Question 2 - Select One
If $x = log θ, θ > 0 and y = \frac{1}{θ}, t h e n \frac{d^{2} y}{{d x}^{2}} =$
A0
B1
C $\frac{d y}{d x}$
D $- (\frac{d y}{d x})$
Question 3 - Select One
If $sec θ - tan θ = \frac{x}{y} (0 < x < y) and 0^{\circ} < θ < 90^{\circ}$ , then $sin θ$ is equal to
A $\frac{y^{2} - x^{2}}{x^{2} + y^{2}}$
B $\frac{x^{2} + y^{2}}{y^{2} - x^{2}}$
C $\frac{2 x y}{x^{2} + y^{2}}$
D $\frac{x^{2} + y^{2}}{2 x y}$

OP TANDON-COORDINATION COMPOUNDS-SBJECTIVE TYPE

Home
Ask Doubt
Profile