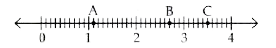Write the complex number represented by the point (-2,5)
The correct Answer is:−2+5i
Step by step video, text & image solution for Write the complex number represented by the point (-2,5) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Assignment (Section -A) (objective Type Questions ( one option is correct)47videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - AAKASH INSTITUTECHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Assignment (Section -B) (objective Type Questions ( one option is correct)78videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - AAKASH INSTITUTECHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - section-J (Aakash Challengers Qestions)16videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - AAKASH INSTITUTECHAPTER - BINOMIAL THEOREMEXERCISE - Assignment (section-J) Objective type question (Aakash Challengers Questions)4videos
BINOMIAL THEOREM
- BOOK - AAKASH INSTITUTECHAPTER - CONIC SECTIONSEXERCISE - SECTION - J ( Aakash Challengers Questions )14videos
CONIC SECTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The conjugate of the complex number represented by the point ( 6-5) is
A6−5iB6+5iC−6+5iD−6−5i
Write the decimal number represented by the points A,B,C,D on the given number line.
 View Solution
View SolutionWrite the decimal number represented by the points on the given number line: A, B, C, D. (Figure)
View SolutionWrite the decimal number represented by the points A, B, C, D on the given number line.
 View Solution
View Solutionwrite the complex numbers that are represented by the following points in the complex plane
(i) 0,3 (ii) (-1 ,0)View SolutionIf z1,z2 are two complex numbers representing two consecutive vertices of a square then what is the complex number represented by the centre of the square ?
View SolutionThe complex number z=(1+i) represented by the point P is Argand plane and OP is rotated an angle of π2 in counter clock wise direction then the resulting complex number is
View SolutionWrite the complex number: √−16
View Solution