Suppose that you are given a system of two equations of the following form
$A cos ϕ = B v_{1} - B v_{2} cos θ$ …………..(1)
$A sin ϕ = B v_{2} sin θ$ ………..(2)
Show that,
$A^{2} = B^{2} (v_{1}^{2} + v_{2}^{2} - 2 v_{1} v_{2} cos θ)$

Video Solution

Text Solution

Verified by Experts

Squaring and adding (1) and (2), we get
$A^{2} ({cos}^{2} ϕ + {sin}^{2} ϕ) = B^{2} [v_{1}^{2} + v_{2}^{2} ({cos}^{2} θ + {sin}^{2} θ)] - v_{1} v_{2} cos θ]$
$A^{2} = B^{2} (v_{1}^{2} + v_{2}^{2}) ({cos}^{2} θ + {sin}^{2} θ)] - v_{1} v_{2} cos θ]$
$A^{2} = B^{2} (v_{1}^{2} + v_{2}^{2} - 2 v_{1} v_{2} cos θ)$

|

Updated on:21/07/2023

Class 12 MATHS TRIGNOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In the following diagram if $V_{2} > V_{1}$ then

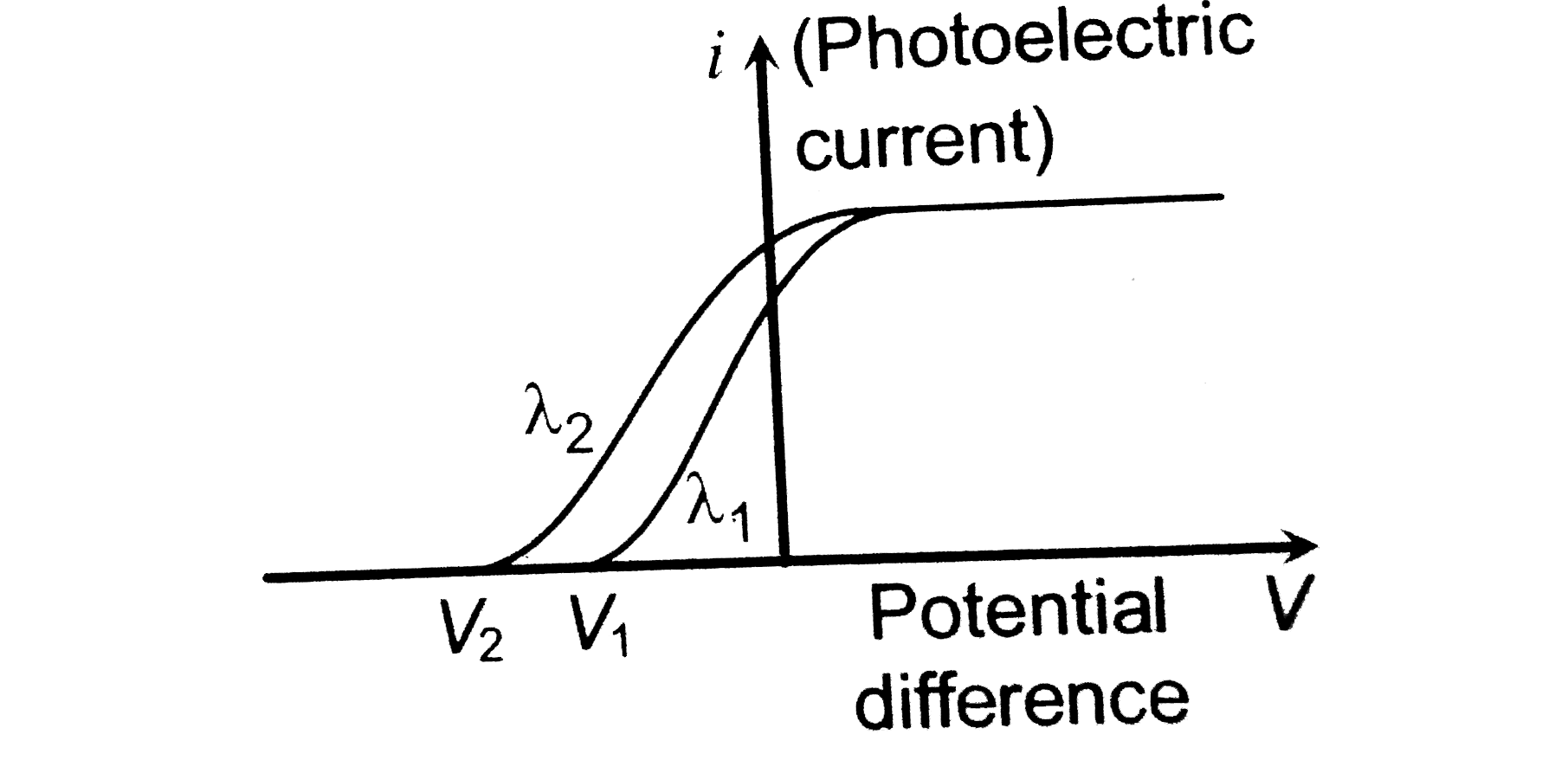A $λ_{1} = \sqrt{λ_{2}}$
B $λ_{1} < λ_{2}$
C $λ_{1} = λ_{2}$
D $λ_{1} > λ_{2}$
Question 2 - Select One
$\frac{{(1 + cos θ)}^{2} + {sin}^{2} θ}{(cos e c^{2} θ - 1) {sin}^{2} θ} =$
A $cos θ (1 + sin θ)$
B $sec θ (1 + sin θ)$
C $2 cos θ (1 + sec θ)$
D $2 sec θ (1 + sec θ)$
Question 3 - Select One or More
Two particles of equal mass in are projected from the ground with speeds $v_{1}$ and $v_{2}$ at angles $θ_{1}$ , and $θ_{2}$ as shown in the figure. Given $θ_{2} > θ_{1}$ and $v_{1} {cos θ}_{1} = v_{2} {cos θ}_{2}$ Which statement/s is/are correct?

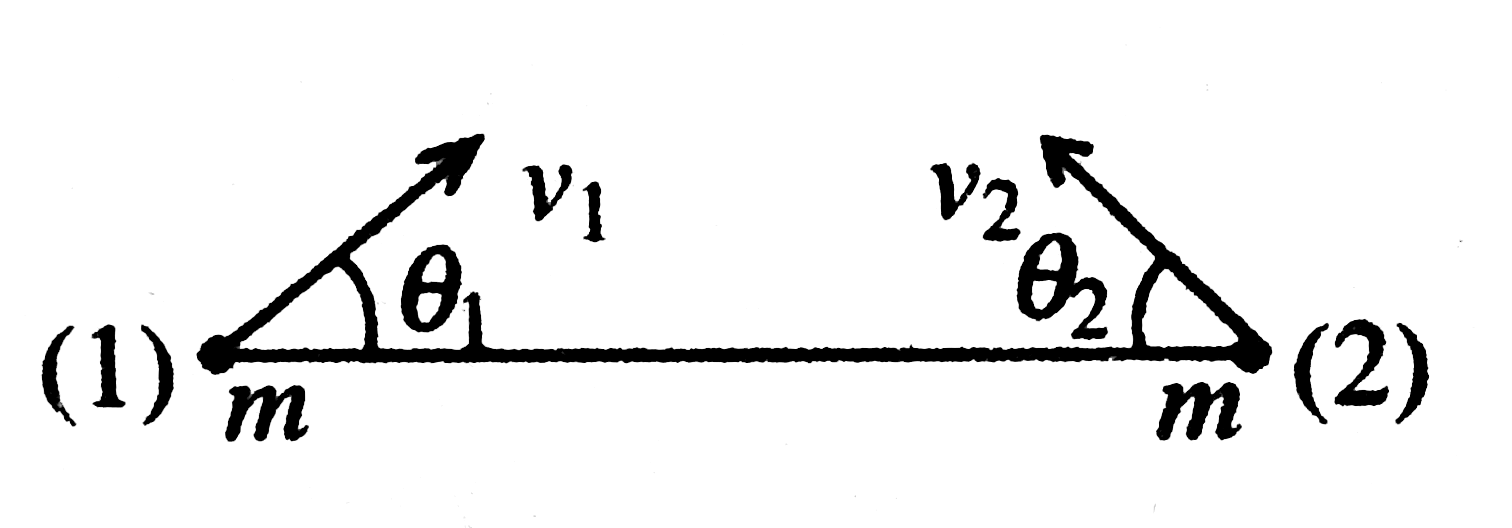ACentre of mass of particles will move along a vertical line.
BCentre of mass of particles will move along a line inclined at some angle with vertical.
CParticle $' 1'$ will be above vertical. centre of mass level when both particles are in air.
DParticle $' 2'$ will be above centre of mass level both particles are in air.

AAKASH INSTITUTE-TRIGNOMETRIC FUNCTIONS -Section - J (Akash Challengers Question)

Home
Ask Doubt
Profile