The radius of the circle touching two sides AB and AC of a triangle ABC and having its center on BC is equal to………………..

Video Solution

Text Solution

Verified by Experts

$\frac{2 Δ}{b + c}$

Updated on:21/07/2023

In the figure shown here, a circle touches the side BC of a triangle ABC at P and AB and AC produced at Q and R respectively. What is AQ equal to ?

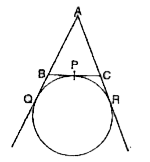AOne-third of the perimeter of $Δ$ ABC.
BHalf of the perimeter of $Δ$ ABC.
CTwo-third of the perimeter of $Δ$ ABC
DThree-fourth of the perimeter of $Δ$ ABC
Let G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If $B C = 6, A C = 8$ , then the length of side AB is equal to
A $\frac{1}{2}$
B $\frac{2}{\sqrt{3}}$
C $5 \sqrt{2}$
Dnone of these
If the radius of the circum-circle of an isosceles triangle ABC is equal to $A B (= A C)$ , then angle A is
A $\frac{π}{6}$
B $\frac{π}{3}$
C $\frac{π}{2}$
D $\frac{2 π}{3}$