Two points charges +4q and +q are separated by distance r, where should a third point charge Q be placed that the whole system remains in equilibrium
2r3 from q
r3 from q
r2 from q
r3 from 4q
The correct Answer is:B
To solve the problem of where to place a third point charge Q such that the whole system remains in equilibrium, we can follow these steps:
Step 1: Understand the System
We have two point charges:
- Charge 1: +4q
- Charge 2: +q
These two charges are separated by a distance r. We need to find the position of a third charge Q such that the net force acting on it due to the other two charges is zero.
Step 2: Define the Position of Charge Q
Let's denote the position of charge Q as being at a distance x from the charge +4q. Consequently, the distance from charge +q will be r−x.
Step 3: Apply Coulomb's Law
According to Coulomb's law, the force between two point charges is given by:
F=k|q1q2|d2
where k is Coulomb's constant, q1 and q2 are the magnitudes of the charges, and d is the distance between them.
Step 4: Calculate the Forces Acting on Charge Q
1. The force F1 exerted on Q by +4q:
F1=k4qQx2
2. The force F2 exerted on Q by +q:
F2=kqQ(r−x)2
Step 5: Set the Forces Equal for Equilibrium
For the system to be in equilibrium, the forces F1 and F2 must be equal in magnitude:
F1=F2
This gives us the equation:
k4qQx2=kqQ(r−x)2
Step 6: Simplify the Equation
We can cancel k and qQ from both sides (assuming Q≠0 and q≠0):
4x2=1(r−x)2
Step 7: Cross-Multiply and Rearrange
Cross-multiplying gives:
4(r−x)2=x2
Expanding the left side:
4(r2−2rx+x2)=x2
This simplifies to:
4r2−8rx+4x2=x2
Rearranging gives:
3x2−8rx+4r2=0
Step 8: Solve the Quadratic Equation
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=3, b=−8r, and c=4r2:
x=8r±√(−8r)2−4⋅3⋅4r22⋅3
Calculating the discriminant:
64r2−48r2=16r2
Thus,
x=8r±4r6
This gives two possible solutions:
1. x=12r6=2r (not valid as it exceeds the distance)
2. x=4r6=2r3
Step 9: Find the Distance from Charge +q
The distance from charge +q will then be:
r−x=r−2r3=r3
Conclusion
The third charge Q should be placed at a distance of r3 from the charge +q (or 2r3 from the charge +4q) for the system to remain in equilibrium.
We have two point charges:
- Charge 1: +4q
- Charge 2: +q
Let's denote the position of charge Q as being at a distance x from the charge +4q. Consequently, the distance from charge +q will be r−x.
According to Coulomb's law, the force between two point charges is given by:
F=k|q1q2|d2
where k is Coulomb's constant, q1 and q2 are the magnitudes of the charges, and d is the distance between them.
1. The force F1 exerted on Q by +4q:
F1=k4qQx2
2. The force F2 exerted on Q by +q:
F2=kqQ(r−x)2
For the system to be in equilibrium, the forces F1 and F2 must be equal in magnitude:
F1=F2
This gives us the equation:
k4qQx2=kqQ(r−x)2
We can cancel k and qQ from both sides (assuming Q≠0 and q≠0):
4x2=1(r−x)2
Cross-multiplying gives:
4(r−x)2=x2
Expanding the left side:
4(r2−2rx+x2)=x2
This simplifies to:
4r2−8rx+4x2=x2
Rearranging gives:
3x2−8rx+4r2=0
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=3, b=−8r, and c=4r2:
x=8r±√(−8r)2−4⋅3⋅4r22⋅3
Calculating the discriminant:
64r2−48r2=16r2
Thus,
x=8r±4r6
This gives two possible solutions:
1. x=12r6=2r (not valid as it exceeds the distance)
2. x=4r6=2r3
The distance from charge +q will then be:
r−x=r−2r3=r3
The third charge Q should be placed at a distance of r3 from the charge +q (or 2r3 from the charge +4q) for the system to remain in equilibrium.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION-C ( OBJECECTIVE TYPE QUESTIONS)1videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH INSTITUTECHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION-D(LINKED COMPREHENSION TYPE QUESTIONS) COMPHREHENSION-13videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH INSTITUTECHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - ASSIGNMENT(SECTION-A) Objective Type Question47videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH INSTITUTECHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)10videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)15videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Two fixed point charges +4e and +e units are separated by a distance a. Where should a third point charge be placed for it to be in equilibrium?
View Solution(a) Two point charges Q and 16Q are fixed at separation d. Where should a third point charge be placed between them so that it experiences no force I.e. in equilibrium ?
(b) In the previous problem , if we replace Q by −Q , where should the third charge be placed on the joining the charges so that it is equilibrium ?
(c ) Three point charges Q,q and Q are placed at x=0,x=d/2 and x=d. Find q in terms of Q so that all charges are in equilibrium.
(d) Two point charges 9Q and 25Q are placed at separation d. Where should a third charge q be placed between them so that all charges are in equilibrium ? Also find the value of q and its nature.View Solution
Knowledge Check
- Question 1 - Select One
Two points charges +4q and +q are separated by distance r, where should a third point charge Q be placed that the whole system remains in equilibrium
A2r3 from qBr3 from qCr2 from qDr3 from 4q - Question 2 - Select One or More
Two point charges Q and −Q/4 are separated by a distance X. Then
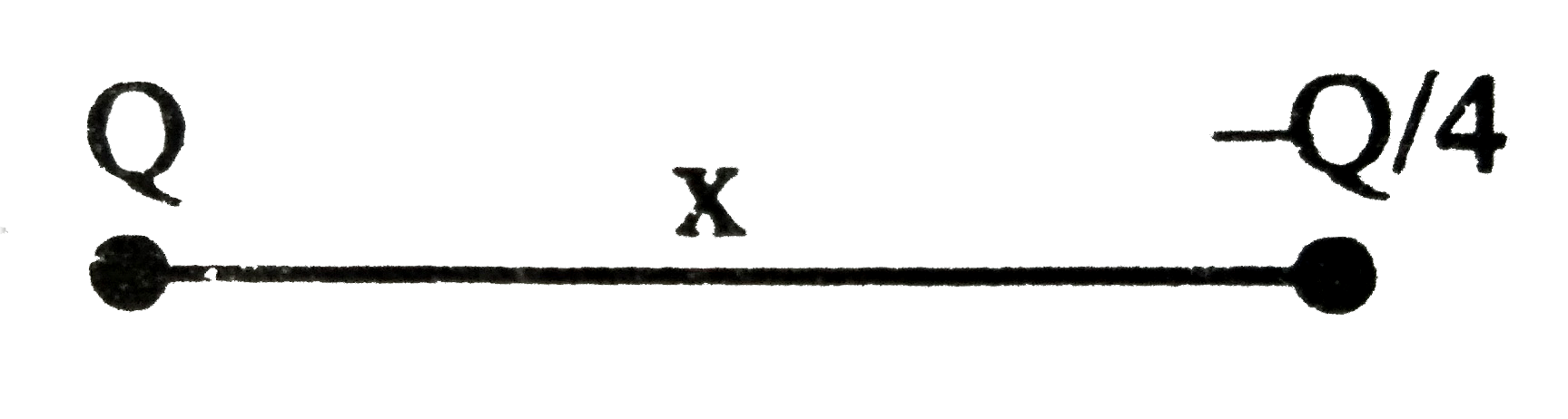 .Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.
.Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero. - Question 3 - Select One
Two point metal charges−q and +2q are placed at a certain distance apart.Where should a third point charge be placed so that it is in equilibrium?
Aon the line joining the two charges on the right of +2qBon the line joining the two charge on the left of −qCbetween −q and +2qDat any point on the right bisector of the 1 line joining −q and +2q
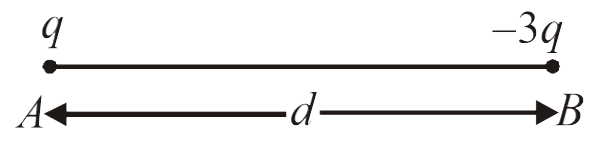
Two charge q and –3q are placed fixed on x–axis separated by distance d. Where should a third charge2q be placed such that it will not experience any force ?
 View Solution
View SolutionTwo charges q and 3q are placed fixed on x-axis separated by distance 'd'. Where should a third charge 2q be placed such that it will not experience any force ?
View SolutionTwo point charges +9e and +e are kept 16cm. Apart from each other. Where should a third charge q be placed between them so that the system is in equilibrium state:
View SolutionTwo point charges 2q and 8q are placed at a distance r apart. Where should a third charge −q be placed between them so that the electrical potential energy of the system is a minimum
View SolutionTwo point charges +4q and +q are placed at a distance L apart. A third charge Q is so placed that all the three charges are in equilibrium. Then location. And magnitude of the third charge will be
View Solution

