Two charges +qand−q, each of mass m, are revoloving in a circle of radius R, under mutal electrostatic force, Find (i) speed of each charge (ii) kinitic energy of the system (iii) potental energy of the system and (iv) total energy of the system.
In this situation, the centripetal force is provided by the electrostatic force of attraction.
(i) By Newton's second law, F=14πε0(2R)2=mv2R
⇒v=√14πε0q2(4R)m

(ii) Kinective energyof the system 12mv2+12mv2=q24πε0(4R)=q216πε0R
(ii) Potential energy of the system =14πε0q(−q)2R=−14πε0q2(2R)=−q28πε0R
(iv) Total energy of the system = K.E. + P.E. =−q24πε0(4R)=−q216πε0R
Note : K.E. ∣∣∣12P.E.∣∣∣,T.E.=P.E.2
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - TRY YOURSELF
110 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT (SECTION-A) Objective Type Questions (Only one answer)
47 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
16 Videos
Similar Questions
Two charges +qand−q, each of mass m, are revoloving in a circle of radius R, under mutal electrostatic force, Find (i) speed of each charge (ii) kinitic energy of the system (iii) potental energy of the system and (iv) total energy of the system.
View SolutionFind the electric potential energy of the system of charges.
(a)
View Solution
Knowledge Check
A particle of mass m and charge -q circulates around a fixed charge q in a circle radius under electrostatic force. The total energy of the system is (k= (14πε0))
A−Kq22rBKq2rC−Kq2rDZeroAn electron of mass m and charge -e moves in circular orbit of radius r round the nucleus of charge +Ze in unielectron system. In CGS system the potential energy of electron is
A+Ze2r2B−Ze2rCZe22rD−Ze22rWhen we bring two electrons close to each other, the electrostatic potential energy of the system:
AIncreasesBBecomes zeroCRemains unchangedDDecreases
If Q charge is given to a sphere of radius R, the energy of the system is
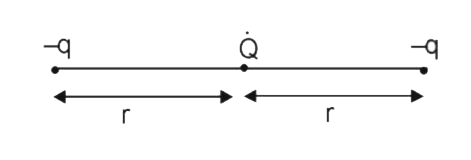
View SolutionThree charges are placed as shown in fig if the electric potential energy of system is zero, then Q : q-
View SolutionIn a solid uniformly charged sphere of total charge Q and radius R, if energy stored out side the sphere is U0 joules then find out self energy of sphere in term of U0 ?
View SolutionA uniformly charged sphere has charge Q. An electron (charge – e, mass m) revolves around it in a circular orbit of radius r. (a) Write the total energy (i.e., sum of its kinetic energy and electrostatic potential energy in the field of the sphere) of the electron. (b) If the time period of revolution of the electron in circular orbit of radius r is T, then find the time period if the orbital radius is made 4r.
View SolutionWhat do you understand by electrostatic potential energy ? Find an expression for electrostatic potential energy of a system of two point charges.
View Solution
