The field potential inside a charged ball of radius R and centre at O depends only on distance from its centre as V(r)=αr2+β when α,β are +ve constant . Now choose correct options
Electric field inside the ball Er=−2αr
Electric flux passing through an imaginary sphere of radius r centre at O will be −2παr2
Volume charge density ρ(r) inside ball is −ε0α
Electric energy of charges ball will be 485πε0α2R5
The correct Answer is:(1,3,4)
To solve the problem, we need to analyze the electric potential V(r) given by the equation:
V(r)=αr2+β
where α and β are positive constants. We will find the electric field E inside the charged ball using the relationship between electric potential and electric field.
Step 1: Understand the relationship between electric potential and electric field
The electric field E is related to the electric potential V by the formula:
E=−dVdr
This means that to find the electric field, we need to take the derivative of the potential with respect to the distance r.
Step 2: Differentiate the potential function
Now we will differentiate the given potential function V(r):
V(r)=αr2+β
Taking the derivative with respect to r:
dVdr=ddr(αr2+β)=2αr+0=2αr
Step 3: Calculate the electric field
Now, substituting this result into the formula for the electric field:
E=−dVdr=−2αr
Step 4: Analyze the result
From our calculation, we find that the electric field inside the charged ball is:
E=−2αr
Since α is a positive constant, the electric field E is directed towards the center of the ball (indicated by the negative sign) and its magnitude increases linearly with r.
Conclusion
The electric field inside the charged ball is given by:
E=−2αr
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-D(COMPREHENSION-I)3videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-E (Assertion-Reason Type Questios)12videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B(OBJECTIVE TYPE QUESTIONS(ONLY ONE ANSWER) )23videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - AAKASH INSTITUTECHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions25videos
ELECTROMAGNETIC WAVES
- BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)16videos
GRAVITATION
Similar Questions
Potential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
View SolutionThe potential energy (U) of diatomic molecule is a function dependent on r (interatomic distance )as U=αr10−βr5−3
Where αandβ are positive constants. The equilrium distance between two atoms will be (2αβ)ab where a=___View Solution
Knowledge Check
- Question 1 - Select One
The electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
A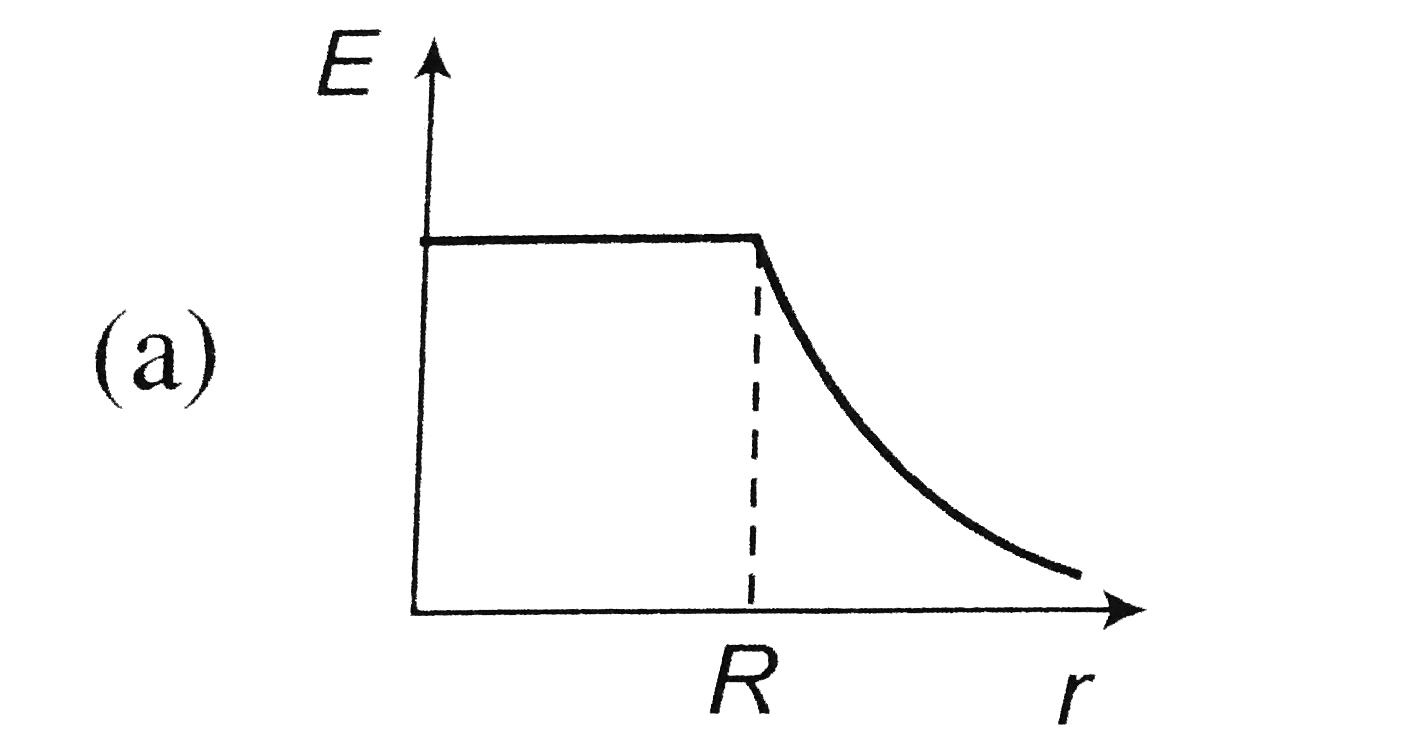 B
B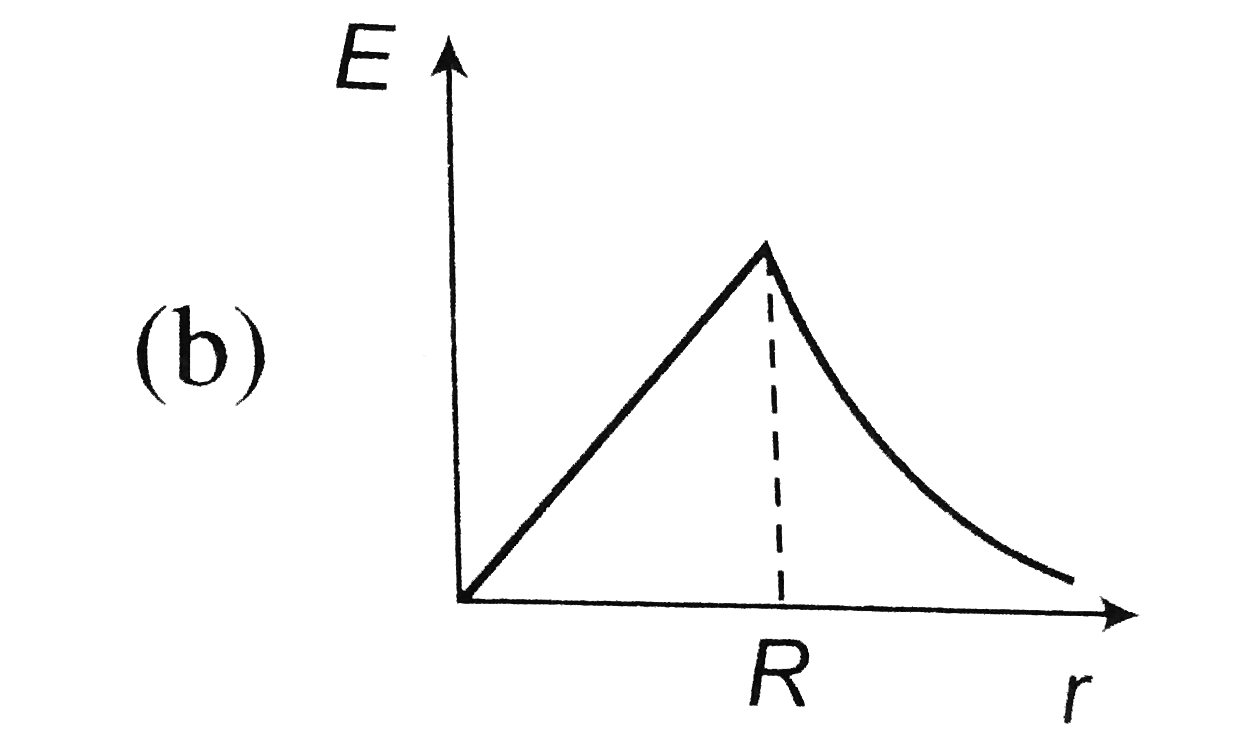 C
C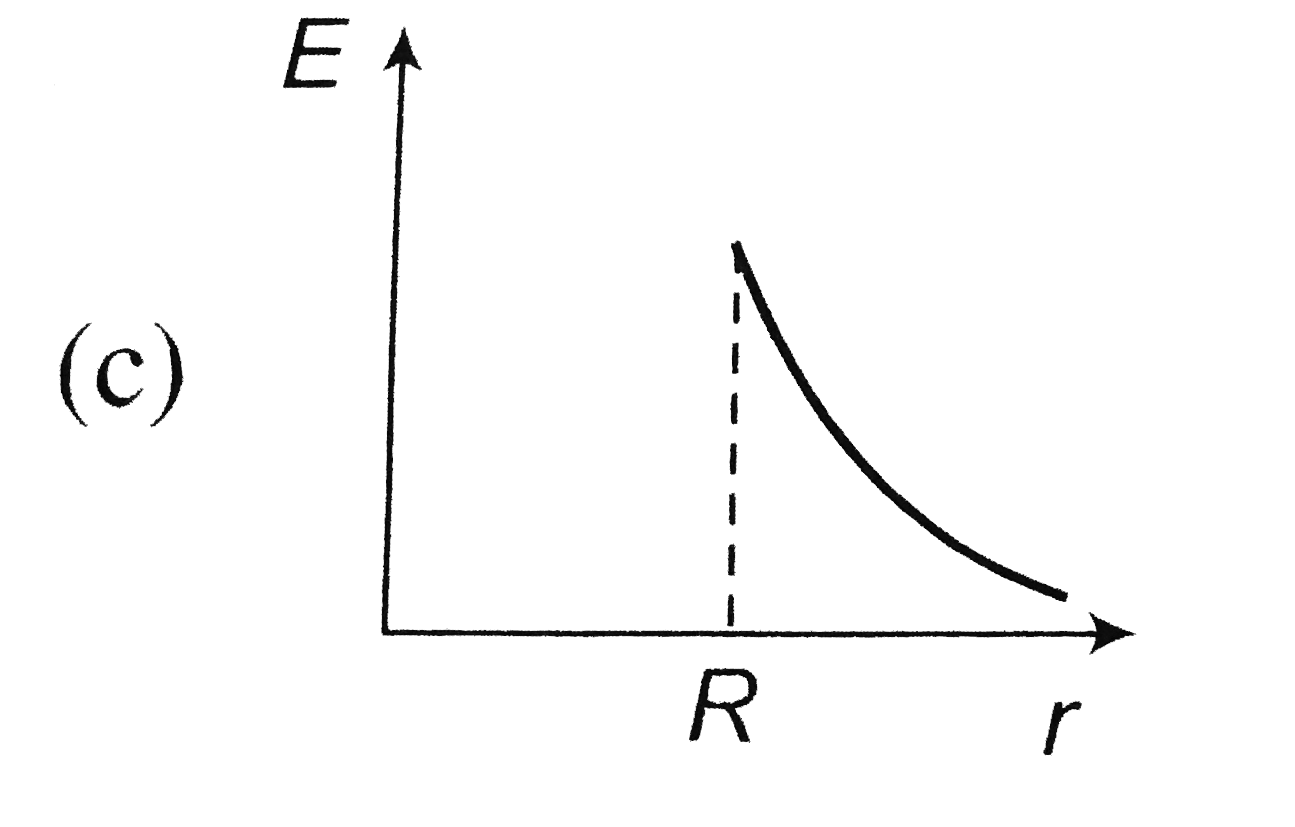 D
D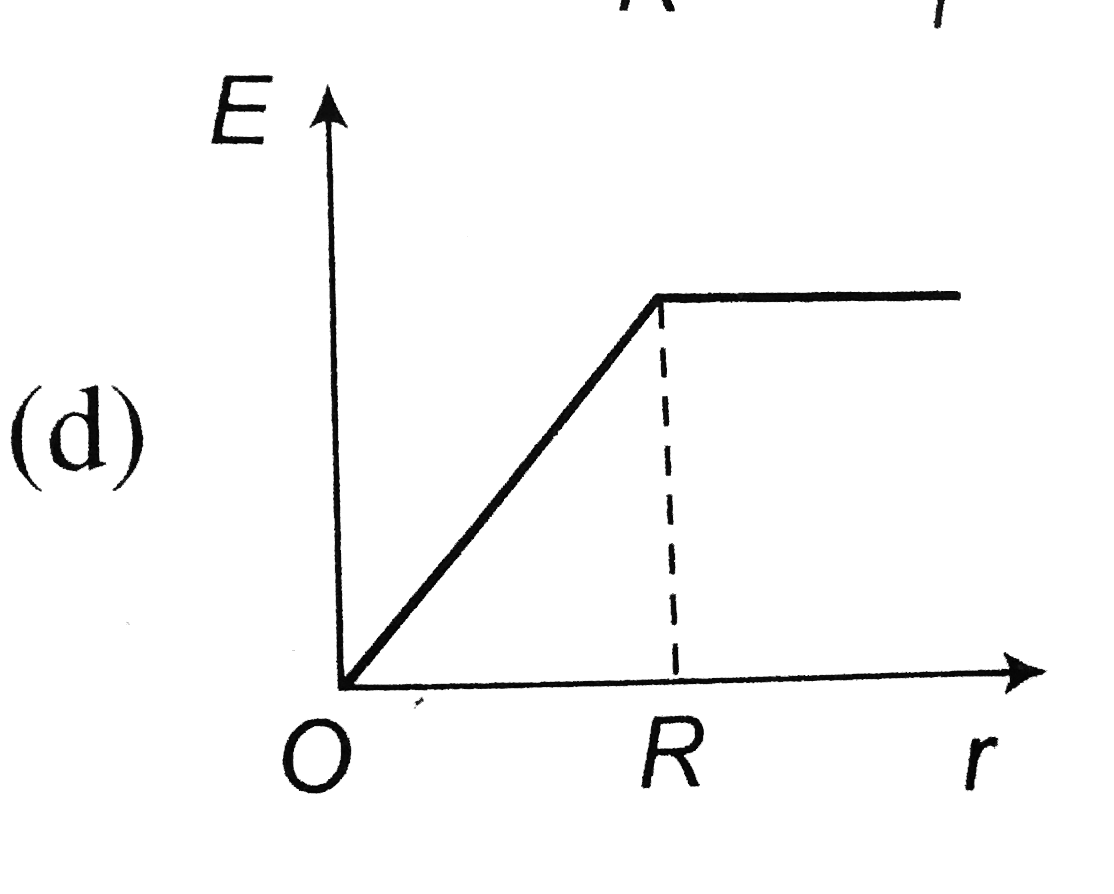
- Question 2 - Select One
The potential inside a charged ball depends only on the distance r of the point form its centre according to the following relation V=Ar2+Bvo<s The charge density inside the ball will be
A−6ε0B6ε0C−3ε0ArD−6ε0Ar - Question 3 - Select One
The electrostatic potential inside a charged spherical ball is given by ϕ=ar2+b where r is the distance from the centre and a, b are constants. Then the charge density inside the ball is:
A(a) −6aε0rB(b) −24πaε0C(c) −6aε0D(d) −24πaε0r
The electrostatic potential inside a charged spherical ball is given by ϕ=ar2+b, where r is distance from the center of the ball, a and b are constants. Calculate the charge density inside the ball.
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionThe electrostatic potential inside a charged spherical ball is given by ϕ=ar2+b where r is the distance from the centre and a, b are constants. Then the charge density inside the ball is:
View SolutionGraphical representation of electric field due to uniformly charged sphere of radius R as function of distance from its centre is given by:
View SolutionThe distance of the centre of mass of a hemispherical shell of radius R from its centre is
View Solution

