A capacitor of capacitance C, charged to a potential difference V, is discharged through a series combination of two resistors R1 and R2. Find the heat generated in resistor R1 during discharging.
CR(1)V22(R1+R2)
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-J10videos
CURRENT ELECTRICITY
- BOOK - AAKASH INSTITUTECHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-H ( MULTIPLE TRUE-FALE TYPE QUESTIONS)5videos
CURRENT ELECTRICITY
- BOOK - AAKASH INSTITUTECHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)10videos
COMMUNICATION SYSTEMS
- BOOK - AAKASH INSTITUTECHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)10videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
A capacitor of capacitance C is charged to a voltage V0 and subsequently discharged through a combination of a resistor R and another identical capacitor C in series. Find the current at time t and heat generated in the same time.
View SolutionA capacitance C charged to a potential difference V is discharged by connecting its plates through a resistance R. Find the heat dissipated in one time constant after the connections are made. Do this by calculating ∫i2Rdtand also by finding the decrease in the energy stored in the capacitor.
View Solution
Knowledge Check
- Question 1 - Select One
A 5.0 uF capacitor is charged to a potential difference of 800 V and discharged through a conductor. The energy given to the conductor during the discharge is
A1.6x10−2JB3.2 JC1.6 JD4.2 J - Question 2 - Select One
A 5.0 uF capacitor is charged to a potential difference of 800 V and discharged through a conductor. The energy given to the conductor during the discharge is
A1.6x10−2JB3.2 JC1.6 JD4.2 J - Question 3 - Select One
Consider two resistors R1 and R2 in series. The current flowing through R1 and R2 is
AR1=/,R2=2/BR1=/2,R2=1/2CR1=/,R2=/DR1=1/2,R2=2/
A capacitor of capacitance C1 is charged to a potential V1 , while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other
Find the total energy stored in the parallel combination of two capacitors.View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.View SolutionA capacitor is charged to a certain potential and then allowed to discharge through a resistance R. The ratio of charge on the capacitor to current in the circuit
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to
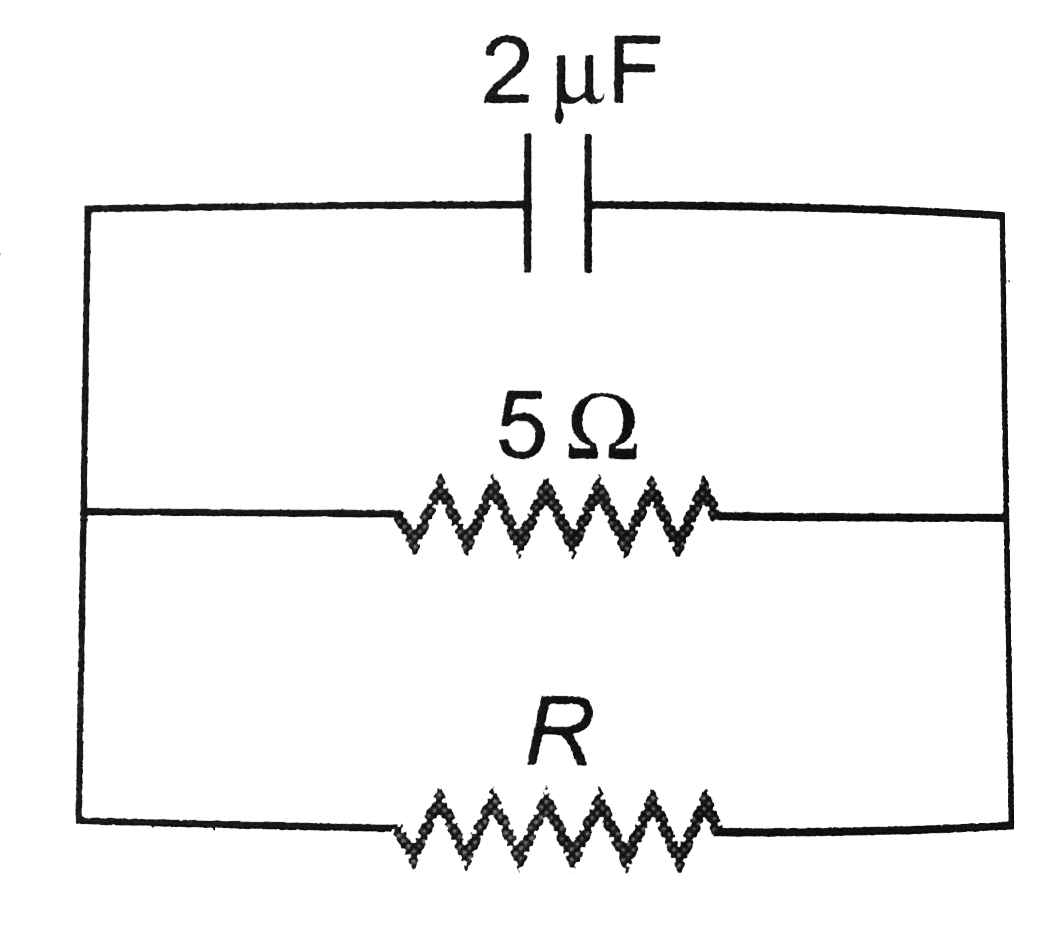 View Solution
View SolutionA capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
View Solution

