If s−x/4= s−y/3=s-z/2 and area of incircle of the triangle XYZ is 8(pi)/3 thenThe radius of the circumcircle of !XYZ
35√6
(352√6
354√6
356√6
s=9,s−x=4s9,s−y=3s9,s−z=2s9 and Δ=6√6
∴x=5,y=6 and z=7
Hence, R=xyz4Δ
⇒R=5×6×74×6√6=354√6
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMACHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - SOLVED MCQ
2 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMACHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Section II - Assertion Reason Type
13 Videos
- PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMBOOK - OBJECTIVE RD SHARMACHAPTER - PROPERTIES OF TRIANGLES AND CIRCLES CONNECTED WITH THEMEXERCISE - Chapter Test
55 Videos
- PLANE AND STRAIGHT LINE IN SPACE BOOK - OBJECTIVE RD SHARMACHAPTER - PLANE AND STRAIGHT LINE IN SPACE EXERCISE - Chapter Test
31 Videos
- REAL FUNCTIONS BOOK - OBJECTIVE RD SHARMACHAPTER - REAL FUNCTIONS EXERCISE - Chapter Test
60 Videos
Similar Questions
The following sentences are the steps involved in construction of the incircle for the triangle XYZ in which ∠Y=90∘,XZ=6 cm and YZ=4 cm.
Arrange them in sequential order from the first to the last.
(A) Mark the foot of the perpendicular from I onto YZ as D.
(B) Construct the triangle XYZ with ∠Y=90∘,XZ=6 cm and YZ=4cm.
(C ) Draw a circle with I as the centre and ID as radius. This is the required incircle.
(D) Draw the bisectors of ∠X,∠Y and ∠Z and mark their point of concurrence as I.
View SolutionIn a triangle XYZ, let x, y, z be the lengths of sides opposite to the angles X, Y, Z, respectively, and 2s = x + y + z. If s−x4=s−y3=s−z2 of incircle of the triangle XYZ is 8π3
View Solution
Knowledge Check
In a !XYZ ,let x , y , z be the length of the side opposite to angles. X , Y, Z respectively and 2s = x + y + z. If s−x4=s−y3=s−z2 and area of the incircle of the triangle XYZ is 8π3, the area of ΔXYZ is
A6√6 sq. unitsB3√6 sq. unitsC12√6 sq. unitsD6√3 sq. unitsIf the difference between areas of the circumcircle and the incircle of an equllateral triangle is 44 cm2, then the area of the triangle is (Take π=227)
A28cm2B7√3cm2C14√3cm2D21cm2If the difference between areas of the circumcircle and the incircle of an equilateral triangle is 44cm2, then the area of the triangle is (Take π=227)
A28cm2B7√3cm2C14√3cm2D21cm2
Construct the incircle for the triangle XYZ in which ∠Y=90∘,XZ=4.5cmandYZ=3cm
View SolutionIf X:Y=3:4,Y:Z=5:2 then find the value of X:Y:Z.
View SolutionIn a ΔPQR (as shown in figure) if x:y:z=2:3:6, then the value of ∠QPR is :
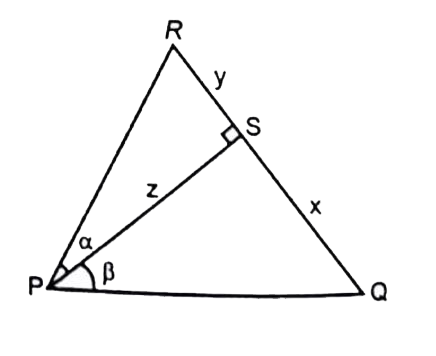
View SolutionΔXYZ is right angled at Y. If ∠X=30∘, then find the value of (cosZ+1/3).
View SolutionIf X:Y=3:4 and Y : Z = 8 : 9 , then X:Y:Z will be :
View Solution
