लम्बाई L तथा l के दो वर्गाकार लूप एक समतल में स्थित है तथा उनके केंद्र सम्पाती (coincident) है यदि l<<L, तो निकाय का अन्योन्य प्रेरकत्व (mutual inductance) ज्ञात करे ।
यदि बड़े लूप से विधुत - धारा I1 प्रवाहित हो, तब इसके केंद्र पर किसी एक भुजा के कारण उत्पन्न चुम्बकीय क्षेत्र,
B0=μ0I14π(L2)(sin45∘+sin45∘)
=μ0I12πL(1√2+1√2)=√2μ0I12πL
∴ सम्पूर्ण लूप के कारण केंद्र पर चुम्बकीय क्षेत्र ,
B=4B0=2√2μ0I1πL
चूँकि l<<L, अतः अंदर वाले वर्गाकार लूप से सम्बन्ध चुम्बकीय फ्लक्स,
ϕ2=BA=2√2μ0I1πLl2.
यदि निकाय का अन्योन्य प्रेरकत्व M हो, तो
ϕ2=MI1
या 2√2μ0I1l2πL=MI1
∴ M=2√2μ0l2πL
Topper's Solved these Questions
Similar Questions
एक चल-कुंडली गैलवेनोमीटर में फेरों की संख्या 50 ,प्रत्येक फेरे का क्षेत्रफल 1.5cm2 और चुम्बकीय क्षेत्र 0.02T है। 10−9A की धारा गैलवेनोमीटर से होकर प्रवाहित करने पर गैलवेनोमीटर से 1 m की दूरी पर रखे स्केल पर 1 cm का विक्षेप उत्पन्न होता है। एकांक ऐठन के बल-आघूर्ण (टॉर्क) का मान निकले।
04:55View Solutionदो वस्तुओ के बिच आवेश विनिमय के क्रम में यदि एक वस्तु दूसरी वस्तु को प्रति सेकण्ड 109 इलेक्ट्रॉन देती हो, तो 1C आवेश देने में कितना समय लगेगा ?
04:21View SolutionL लम्बाई की एक छड़ जिसके सिरे दो परस्पर लम्ब रेखाओं पर स्थित है , फिसलती है । छड़ को 1:2 के अनुपात में विभाजित करने वाले बिंदु का बिन्दुपथ ज्ञात कीजिए ।
04:19View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
03:39View Solutionएक स्थिर आयतन वाले खुले टैंक का आधार वर्गाकार है। यदि अंत: पृष्ठ न्यूनतम हो, तब टैंक कि गहराई तथा लम्बाई का अनुपात ज्ञात कीजिए।
03:14View Solutionसंलगन आकृति में AT और BT दो स्पर्श रेखाएं है तथा वृत्त का केंद्र O है। यदि ∠AOT=55∘ हो ,तो ∠APB का मान क्या होगा ?
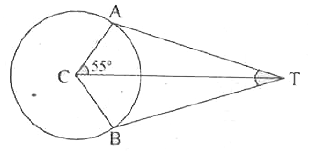 05:19View Solution
05:19View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
05:44View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
04:29View Solutionयदि बिन्दु (2,α,β) उस समतल पर स्थित है, जो बिन्दुओ (3,4,2) तथा (7,0,6) से होकर जाता है तथा समतल 2x−5y=15 के लंबवत है, तो 2α−3β बराबर है
04:55View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
03:30View Solutionयदि रेखा x−32=y+2−1=z+43, समतल lx+my−z=9 में स्थित है, तो l2+m2 बराबर है
03:43View Solutionयदि बिन्दु (4, 2) का रेखा L = 0 के सापेक्ष प्रतिबिम्ब (-2, 6) है, तो L का समीकरण है
04:14View Solutionएक समतल निर्देशाक्षों को क्रमश: A, B तथा C पर काटता है। यदि △ABC का केन्द्रक (2,-1, 3) है, तो समतल का समीकरण ज्ञात कीजिए।
42:04View Solutionउस गोले का समीकरण ज्ञात कीजिए जो बिंदुओं ( 1,0,0), ( 0,1,0) तथा ( 0,0,1) से होकर जाता है तथा जिसका केंद्र समतल 3x−y+z=2पर स्थित है।
50:53View Solutionअन्योन प्रेरण तथा प्रेरकत्व | दो समतल वृत्ताकार कुंडलियों के बीच अन्योन प्रेरकत्व
41:51View Solution

