ड्युटीरियम - ट्रीरियम अभिक्रिया
21H+31H→42H+10n में
(a) निम्नलिखित आँकड़ो का उपयोग कर अभिक्रिया में मुक्त ऊर्जा का मान ज्ञात करे |
m(21H)=2.014102u,<br> m ( "" _ 1 ^ 3H) = 3.016049 u, <br>m (""_2^4 He) = 4.002603 u,<br> m _ n = 1.008665 u .
(b) ड्यूटीरियम तथा ट्रीटियम दोनों की प्रभावी त्रिज्य 2 fm मानकर कूलॉम प्रतिकर्षण से पार पाने के लिए आवशयक गतिज ऊर्जा की गणना करे |
(c) अभिक्रिया को प्रारम्भ करने के लिए गैसों की किस ताप तक गर्म किया जाता होगा ?
ड्यूटीरियम - ट्रीटियम (D-T ) अभिक्रिया है :
21H+31H→42He+10n+Q
(a) दृव्यमान- क्षति
Δm={m(21H)+m(31H)}−{m(42He)+mn}
=(2.014102u+3.016049u)−(4.002603u+1.008665u)
=0.018883 u
∴ मुक्त ऊर्जा,
Q=0.018883×931.5MeV=17.59MeV.
(b) यहाँ ड्यूटीरियम की प्रभावी त्रिज्या R1=2fm=2×10−15 m
और ट्रीटियम की प्रभावी त्रिज्या ,R2=2fm=2×10−15m
दोनों नाभिको के संस्पर्श की स्थिति में विद्युत् स्थितिज ऊर्जा के सूत्र,
U=14π∈0Q1Q2r से,
U=14π∈0e2(R1+R2)
=(9×109Nm2C−2)(1.6×10−19C)2(2×10−15m+2×10−15m)
=5.76×10−14J.
D-T निकाय की यह स्थितिज ऊर्जा टक्कर (collision ) के पहले की नाभिको की कुल गतिज ऊर्जा के बराबर है | अतः नाभिको की आवश्यक गतिज ऊर्जा = 5.76×10−14 J .
(c) यदि दोनों निकाय गैसों का ताप T है, तो दोनों गैसों के प्रत्येक परमाणु की औसत गतिज ऊर्जा = 32kT, जहाँ k वोल्ट्जमान नियतांक है |
∴ दोनों परमाणुओं की कुल गतिज ऊर्जा = 2×32kT=3kT .
परन्तु, नाभिक ( परमाणुओं ) की कुल गतिज ऊर्जा =5.76×10−14J
∴T=5.56×10−14J3×1.38×10−23JK−1=1.39×109K.
Topper's Solved these Questions
Similar Questions
किसी परमाणु के दो ऊर्जा स्तरों में 2.3eV का अंतराल है। यदि परमाणु में संक्रमण उच्च स्तर से निम्न स्तर में होता है, तो उतसर्जित विकिरण की आवृत्ति क्या होगी ?
02:05View Solutionरेडियम के रेडियोऐक्टिव नियतांक की गणना करें जिसकी अर्ध-आयु 1620 वर्ष है।
06:11View SolutionIf l1,(\ m)1,(\ n)1(\ and\ l)2,(\ m)2,n2 be the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of them are (m1(\ n)2−m2n1),\ (n1l2−n2l1),\ (l1m2−l2m1).
01:56View SolutionCalculate the Q-values of the following fusion reactions:
(a)_1^2H+_12H→_1^3H+_11H.
_1^2H+_12H→_2^3(He)+n<br>_12H+_1^3H rarr _24(He)+n.
Atomic masses are m(_1^2H)=2.014102 u, m(_13H)=3.016049u,m(_2^3(He))=3.016029 u, m(_24(He))=4.002603u.05:36View SolutionIn the following reaction the value of 'X' is. ._7 N^14 + ._2 He^4 rarr X + ._1 H^1 .
03:14View SolutionIn the reaction .21H+.31H→.42He+.10n, if the binding energies of .21H,.31H and .42He are respectively a,b and c (in MeV), then the energy (in MeV) released in this reaction is.
02:06View Solutionनीचे के चित्र में m∣∣n और p∣∣q यदि ∠1=75∘ तो साबित करें कि
∠2=∠1+ एक समकोण का 13
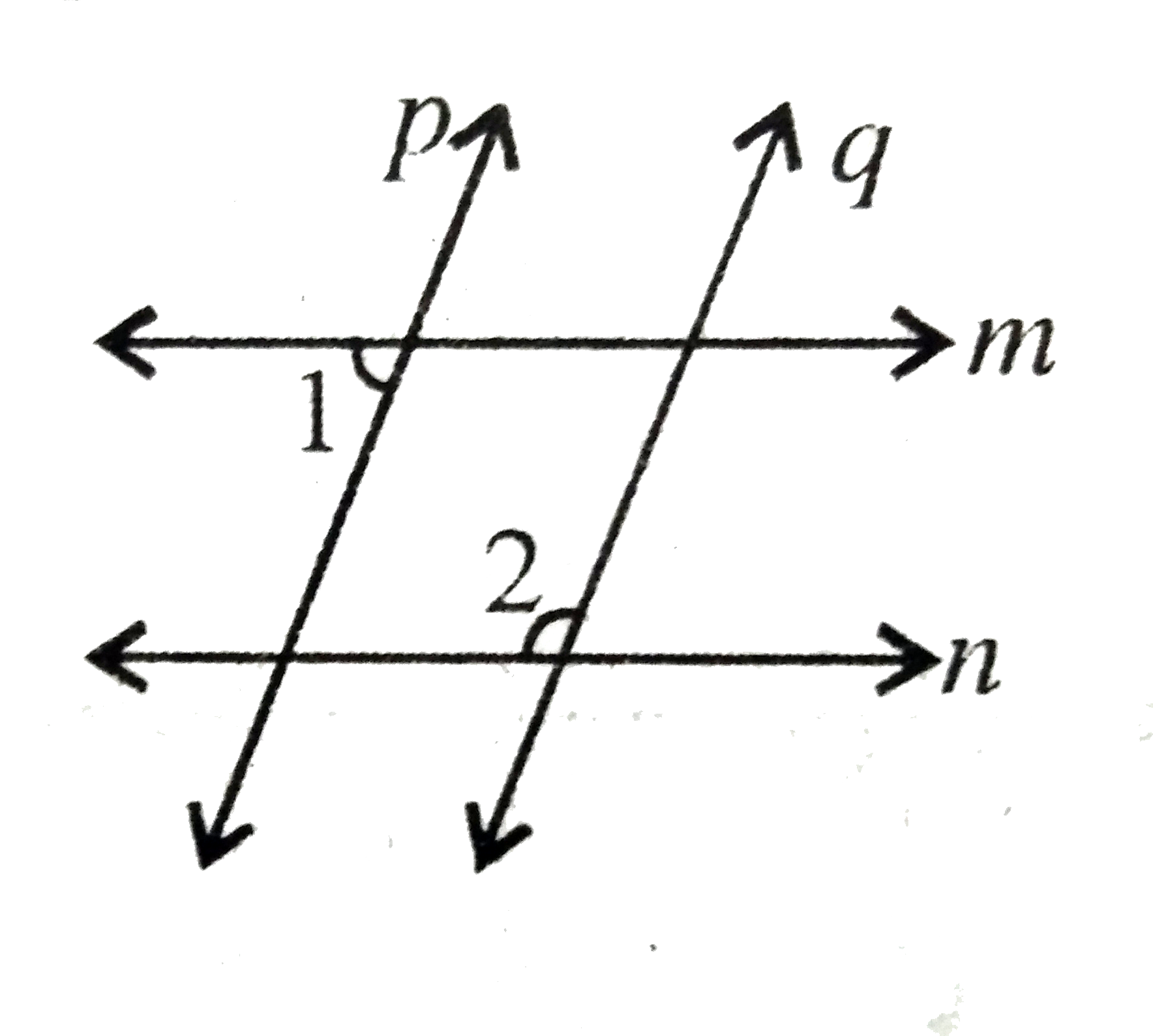 01:19View Solution
01:19View Solution11H+11H+11H+11H→42He+2 __________ [ শূন্যস্থান পূরণ করো ]
03:57View Solution[H21Hand31H] will have the same
03:26View Solutionकथन:- संलयन अभिक्रियाओं के लिए H तथा H उपयुक्त होता है
कारण :- .21H तथा .31H की प्रति न्यूक्लिऑन बंधन ऊर्जा कम होती है।View SolutionIf ,l1,m1,(\ n)1(\ and\ l)2,m2,n2 be the direction cosines of two lines, show that the directioin cosines of the line perpendicular to both them are proportional to (m1(\ n)2−m2n1),\ (n1l2−n2l1),\ (l1m2−l2m1)
03:10View SolutionIn the reaction .21H+.31H→.42He+.10n. If the binding energies of .21H,.31H and .42He are respectively a, b and c (in MeV), then the energy (in MeV) released in this reaction is
01:21View SolutionIn the reaction ._1^2 H + ._1^3 H rarr ._2^4 He + ._0^1 n , if the binding energies of ._1^2 H, ._1^3 H and ._2^4 He are respectively a,b and c (in MeV), then the energy (in MeV) released in this reaction is.
01:18View Solutionनिम्नलिखित में प्रत्येक का मान ज्ञात कीजिए-
(47)−201:35View Solutionनिम्नलिखित में प्रत्येक का मान ज्ञात कीजिए-
(23)−303:10View Solution

