For an ideal diatomic gas, during any process T=KV, find out the molar heat capacity of the gas during process (neglecting vibrational degree of freedom)
A
3R2
B
5R2
C
7R2
D
2R
Video Solution
Text Solution
The correct Answer is:C
T=KV⇒PV0= constant
C=Rγ−1−Rn−1=R75−1−R0−1=5R2+R
7R2
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - STOICHIOMETRY AND BALANCING REDOX REACTION EXERCISE - SINGLE INTEGER ANSWER TYPE QUESTIONS5videos
STOICHIOMETRY AND BALANCING REDOX REACTION
- BOOK - FIITJEECHAPTER - THERMODYNAMICS AND THERMOCHEMISTRY EXERCISE - SINGLE INTEGER ANSWER TYPE QUESTIONS5videos
THERMODYNAMICS AND THERMOCHEMISTRY
Similar Questions
Knowledge Check
- Question 1 - Select One
For an ideal monoatomic gas during any process T = kV, find out the molar heat capacity of the gas during the process. (Assume vibrational degree of freedom to be active)
A52RB3RC72D4R - Question 2 - Select One
For an ideal monoatic gas during any process T=kV, find out the molar heat capacity od the gas
during the process. (Assme vibrational degree of freedom to be active )\A52RB3RC75RD4 R - Question 3 - Select One
The molar heat capacity of a gas in a process
Ais either CVorCPBlies between CVorCPCmay range from zero to infinityDcan have any real value
Ideal mono-atomic gas is taken through process such that dQ = 3dU. The molar heat capacity for process is:
View SolutionP-V diagram of a diatomic gas is a straight line passing through origin. The molar heat capacity of the gas in the process will be
View SolutionOne mole of an ideal gas undergoes a process such that P∝1T. The molar heat capacity of this process is 4R.
View SolutionP - V diagram of a diatomic gas is a straight line parallel to P-axis. The molar heat capacity of the gas in the process will be
View SolutionThe pressure P of an ideal diatomic gas varies with its absolute temperature T as shown in figure. The molar heat capacity of gas during this process is [R is gas constant]
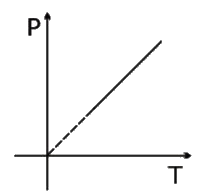 View Solution
View Solution

