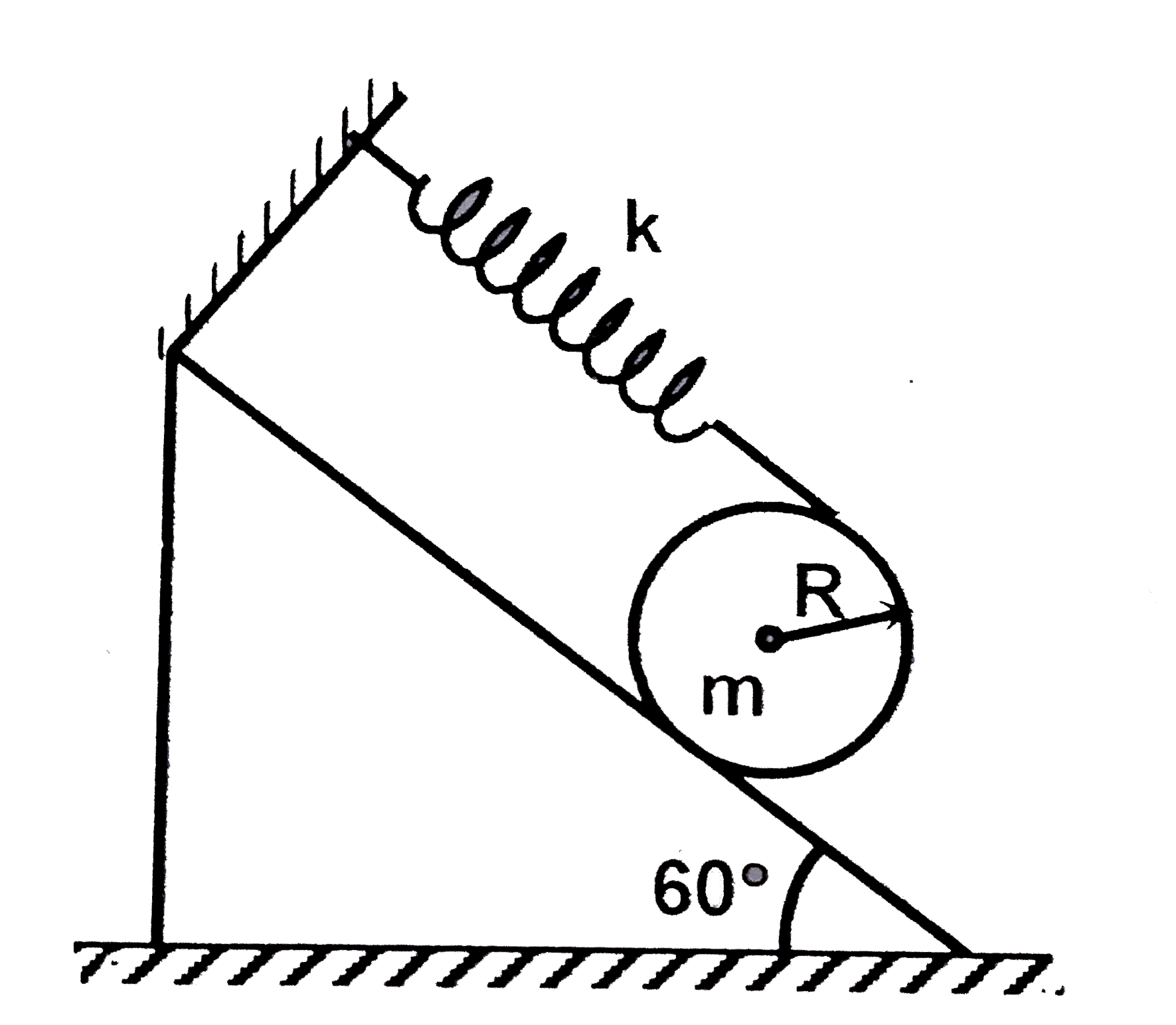
A uniform solid sphere of mass 'm' and radius R is in equilibrium on an inclined plane by the action of the light spring of stiffness k, gravity and on it. If the angle of inclination of the plane is 60∘, then find the time period of oscillation for small displancement.
2π√m10k
2π√7m10k
2π√7m20k
2π√7m40k
The correct Answer is:C
τP=k(2Rθ)2R
IPα=−4kR2θ
75mR2α=−4kR2θ
α=−(207km)θ
T=2π√7m20k
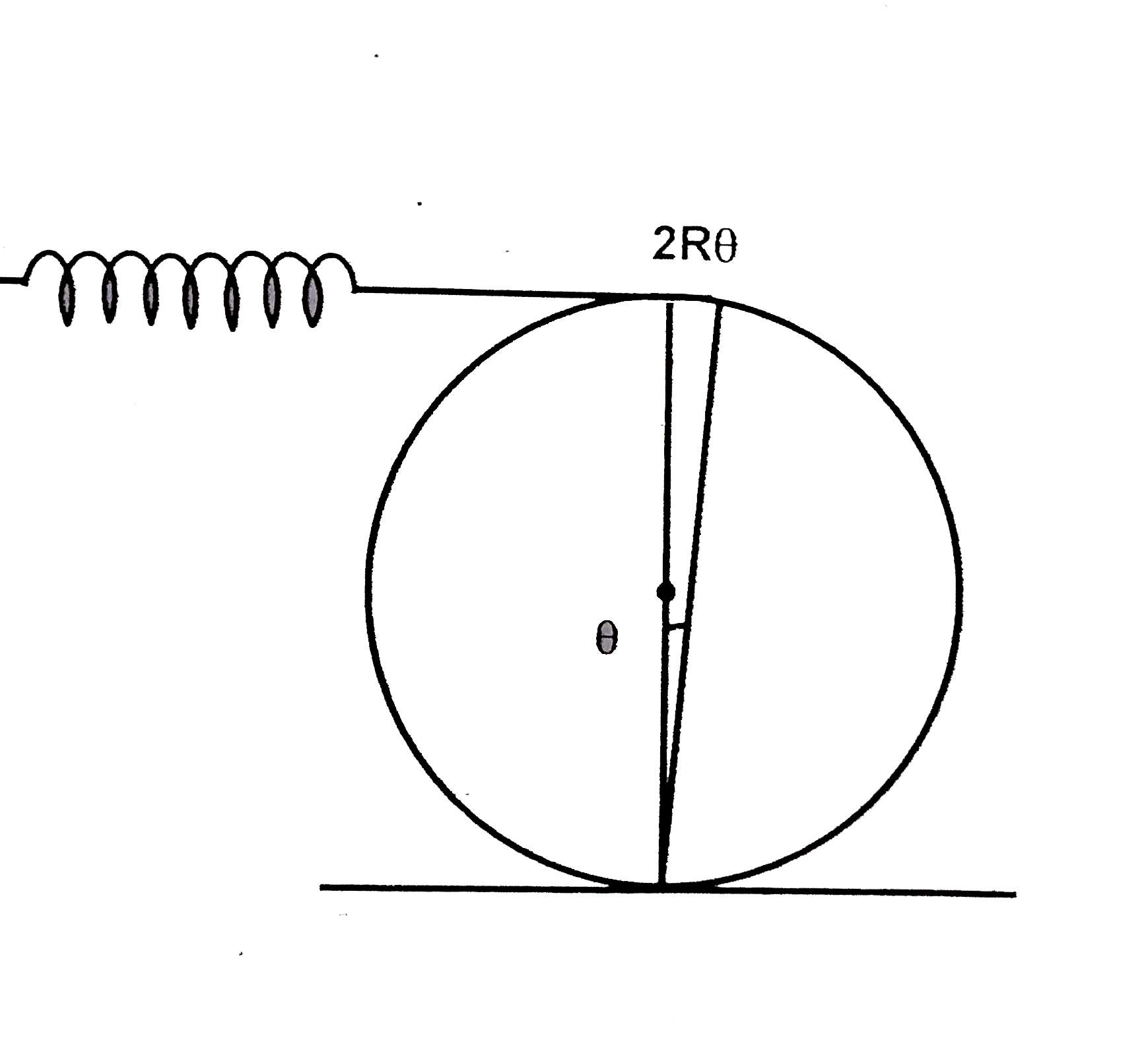
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
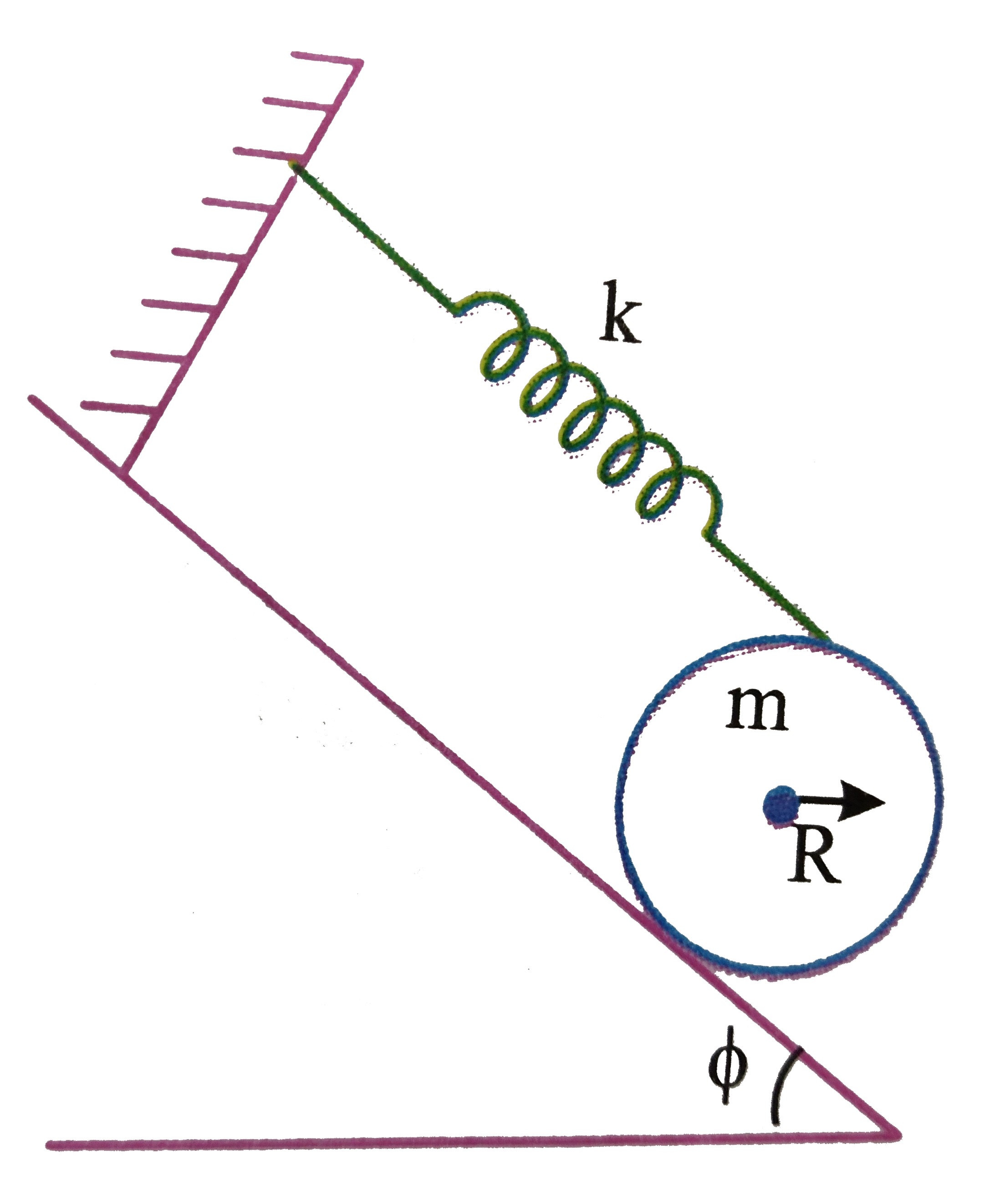
A uniform cylinder of mass m and radius R is in equilibrium on an inclined by the action of a light spring of stiffness, gravity and reaction force acting on it .If the angle of inclination of the plane is ϕ , find the angular frequency of small oscillation of the cylinder

View SolutionA solid sphere having mass m and radius r rolls down an inclined plane. Then its kinetic energy is
View Solution
Knowledge Check
A uniform cylinder of mass m and radius R is in equilibrium on an inclined plane by the action of a light spring of stiffness k, gravity and reaction force acting on it. If the angle of inclination of the plane is ϕ, then angular frequency of small oscillations of the cylinder is...........
 A2√kmB2√2kmC2√2k3mD√2km
A2√kmB2√2kmC2√2k3mD√2kmA disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
A76B54C32Ddepends on angle of inclinationA uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
A2π√rgB2pi sqrt((5 R)/(3 g))C2π√7R5gD2π√2R5g
A solid sphere of mass m rolls down an inclined plane a height h. Find rotational kinetic energy of the sphere.
View SolutionA uniform sphere of mass m and radius R start rolling without slipping down an inclined plane. Find the time dependence of the angular. How will the result be affected in the case of a perfectly smooth inclined plane? The angle of inclination of the plane is θ.
View SolutionA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View SolutionA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
View SolutionIn the adjacent figure, if the incline plane is smooth and the springs are identical then the period of oscillation of this body is

View Solution
