If Q=4v3+3v2, then the value of 'v' such that,there exist maxima of 'Q'-
0
−12
12
none
The correct Answer is:B
Q=4V3+3V2
dQdv=12V2+6V
dQdv=0⇒V=0,−12
d2QdV2=24v+6⇒(d2Qdv2)v=0=6(+ve)
(d2Qdv2)v=−1/2=−12+6=−6(−ve)
V=−1/2 for maximum Q
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 2 PHYSICS1videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP NO. 5 Physics6videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
Knowledge Check
- Question 1 - Select One
If u : v = v : w, then what is the value of u4:v4?
Au2:WvBu2:w2Cu2:w2Du:w - Question 2 - Select One
If 3u + 2v = 7 and uv = 2 then find the value of 3u - 2v.
A±2B±1C−2D2 - Question 3 - Select One
The matrices
P[(u1,v1,w1),(u2,v2,w2),(u3,v3w3)]andQ=19⎡⎢⎣22112−5m−815⎤⎥⎦
are such that PQ=l, an identify matrix. Solving the equation ⎡⎢⎣u1v1w1u2v2w2u3v3w3⎤⎥⎦⎡⎢⎣xyz⎤⎥⎦=⎡⎢⎣115⎤⎥⎦, the value of y comes out to be -3, then the value of m is equal toA27B7C−27D−7
A point moves with uniform acceleration and v1,v2,v3 denote the average velocities in the successive intervals of times v1,v2,v3 . Then v1−v2v2−v3=t1+t2t2+t3
View SolutionIf the rms value of the voltage of the waveform shown below is √pqV , then what is the value of (p+q) ? (p and q are the smallest positive integers.)
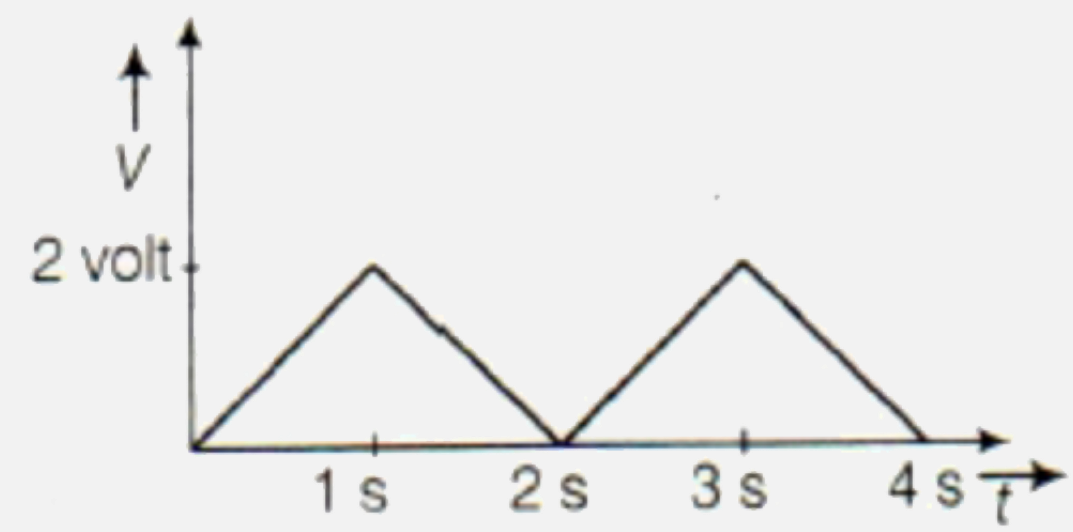 View Solution
View SolutionConsider the following statements.
p : if 7 is an odd number , then 7 is divisible by 2.
Q : If 87 is a prime number , then 7 is an odd number .
if V1 is the truth value of contrapositive of p and V2 is the truth value of conirapositive of Q, then the ordered pair (V1,V2) equals.View SolutionConsider the following two statements:
P : If 7 is an odd number, then 7 is divisible by 2.
Q : If 7 is a prime number, then 7 is an odd number.
If V1 is the truth value of the contrapositive of P and V2 is the truth value of contrapositive of Q then the ordered pair (V1,V2) equals:View SolutionConsider the following two statements:
P: If 7 is an odd number , then 7 is divisible by 2
Q: If 7 is a prime number , then 7 is an odd number .
If V1 is the truth value of the contrapositive of P and V2 is the truth value of contrapositive of Q, then the ordered pair (V1,V2) equals:View Solution

