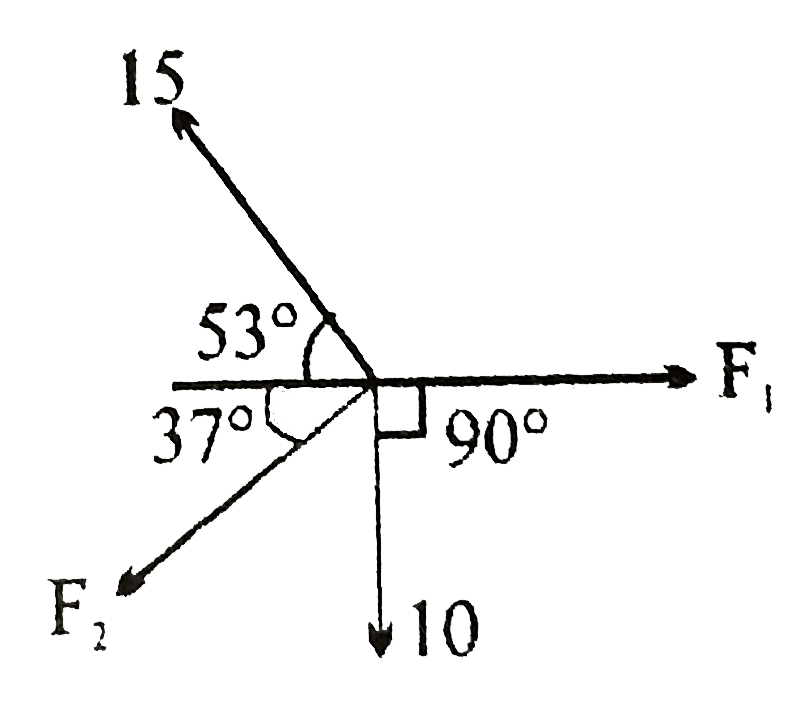
Find the magnitude of the unknown forces X and Y if sum of all forces is zero.

The correct Answer is:(5,10)

Σ→F=0
⇒(ycos37∘ˆi+ysin37∘ˆj)+(5cos53∘(−ˆi)+5sin53∘ˆj)+(x(−ˆi))+10(−ˆj))=0
⇒(4y5−3−x)ˆi+(3y5+4−10)ˆj=0ˆi+0ˆj
Comparting coefficients of ˆi&ˆj both sided - 4y5−x=3 .......(i)
3y5=6⇒y=10
Putting 8−x=3⇒x=5
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Dpp no 10 physics
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Dpp no 11 physics
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 8 PHYSICS
7 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Knowledge Check
Two forces, with equal magnitude F, act on a body and the magnitude of the resultant force is F3. The angle between the two forces is:
Acos−1(−1718)Bcos−1(−13)Ccos−1(23)Dcos−1(89)Two forces with equal magnitudes F act on a body and the magnitude of the resultant force is F /3. The angle between the two forces is
Acos−1(−1718)Bcos−1(−13)Ccos−1(23)Dcos−1(89)Suppose F,FN&f are the magnitudes of the contact force, normal force and the frictional force exerted by one surface on the other, kept in contact, if none of these is zero :
AF>fBFN>fCF>FND(FN−f)<(FN+f)
Find the values of the unknowns x , y , z.
View SolutionFind the values of the unknowns x and y in the following diagrams
View SolutionTwo forces of magnitudes P and Q are inclined at an angle (θ). The magnitude of their resultant is 3Q. When the inclination is changed to (180∘−θ), the magnitude of the resultant force becomes Q. Find the ratio of the forces.
View SolutionTwo parallel forces F1 and F2 acting in the same direction are applied to a rigid body.
Porve that
(a) the magnitude of the resultant force is equal to the sum of magnitudes of the forces being added,
(b) the resultant force is parallel to the forces being added and acts in the same direction,
(c ) the resultant force passes through the centre of the parallel forces, i.e. through the point which divides the distance between the points of application of both forces into sections inversely proportional to the magnitude of the forces.
View SolutionLet F,FNandf denote the magnitudes of the contact force, normal force and the friction exerted by one surface on the other kept in contact. If none of these is zero,
View Solution