A particle is projected with a speed 10√2 making an angle 45∘ with the horizontal . Neglect the effect of air friction. Then after 1 second of projection . Take g=10m/s2.
the height of the aprticle above the point of projection is 5m.
the height of the particle above the point of projection is 10m.
the horizontal distance of the particle from the point of projection is 5m.
the horizontal distance of the particle from the point of projection is 15m.
The correct Answer is:A
y=uxt−12.gt2=10×1−5×12=5m
x=uxt=10×1=10m
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 16 physics8videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 177videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP NO. 14 PHYSICS10videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle of mass m=1kg is projected with speed u=20√2m/s at angle θ=45∘ with horizontal find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View Solution
Knowledge Check
- Question 1 - Select One
A particle is projected with a speed 10√2ms−1 and at an angle 45∘ with the horizontal. The rate of change of speed with respect to time at t=1s is (g=10ms−2)
A10√2ms−2B10ms−2CzeroD5ms−2 - Question 2 - Select One
A particle is projected with speed 10m/s at angle 60∘ with the horizontal. Then the time after which its speed becomes half of initial.
A12 secB1 secC√3/2secD√3/2sec - Question 3 - Select One
A ball is projected with 20√2m/s at angle 45∘ with horizontal.The angular velocity of the particle at highest point of its journey about point of projection is
A0.1rad/sB1rad/sC0.3rad/sD0.4rad/s
A particle is projected with a velocity of 10√2m/s at an angle of 45∘ with the horizontal. Find the interval between the moments when speed is √125m/s(g=10m/s2)
View SolutionA particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s(g=10m/s2) match the following table
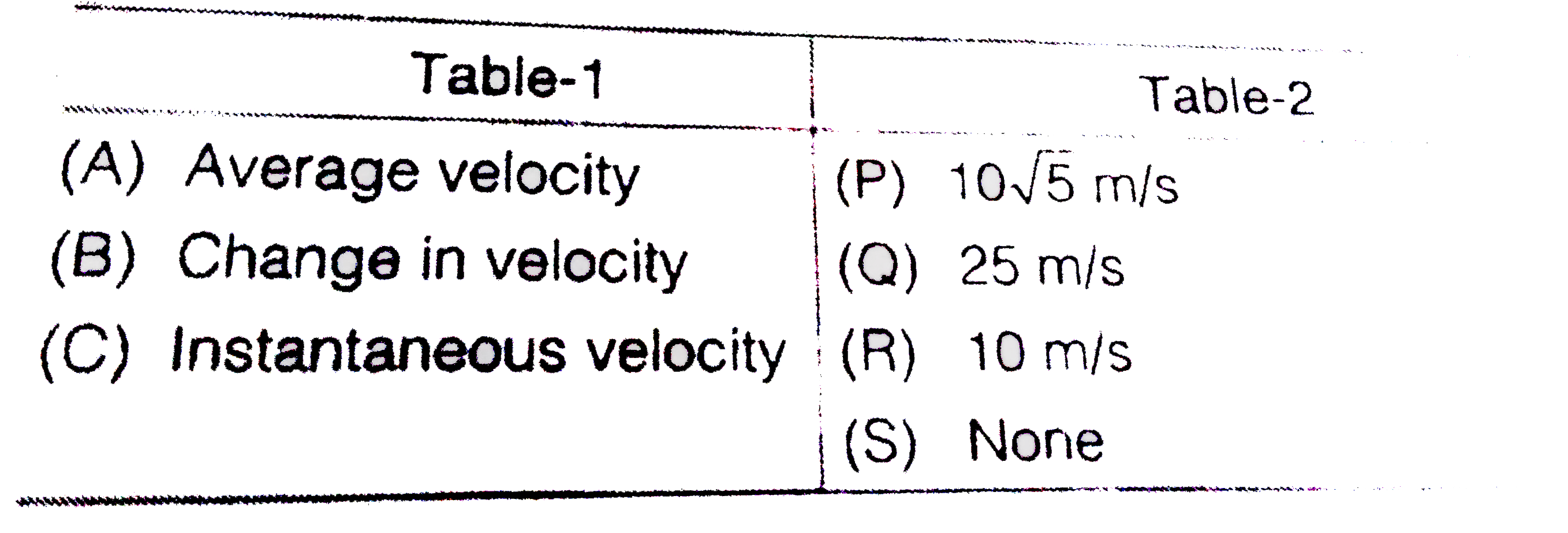 View Solution
View SolutionAn object is projected from ground with speed 20 m/s at angle 30∘ with horizontal. Its centripetal acceleration one second after the projection is
[ Take g = 10 m/s2 ]View SolutionA particle is projected with velocity 10m/s at an angle of 45∘ with the horizontal from some height. Consider point of projection as origin and motion in xy plane. Then (→g=10ˆjm/s2)
View SolutionAn object of mass 10 kg is projected from ground with speed 40 m/s at an angle 60∘ with horizontal the rate of change of momentum of object one second after projection in SI unit is
[ Take g = 9.8 m/s2 ]View Solution

