A particle which is initially at rest at the origin, is subjection to an acceleration with x− and y− components as shown. After time t=5 , the particle has no acceleration.

When is the particle at its farthest distance from the y− axis ?
3sec.
2sec.
4sec.
1sec.
The correct Answer is:C
At,t=2sec(t=2sec)
vx=ux+axt=0+10×2=20m/s
vy=uy+ayt=0−5×2=−10m/s
v=√v2x+v2y=√(20)2+(−10)2=10√5m/s
From t=0,t=4sec
x[12(10)(2)2](0→2)+[(10×2)2−12(10)(2)2](2→4)
x=40m
y=[−125(2)2](0→2)−[(10)(2)−12(10)(2)2](2→4)
y=−10m
Hence , average velcoity of particle between t=0 to t=4sec is
vav=ΔxΔt=√(40)2+(−10)24
vav=52√17m/s
At,t=2sec,u=10×2=20ms
After t=2sec
v=u+at
0=20−10t
t=2sec.
Hence, at t=4 . the particle is at its farthest distance from the y−axis.
The particle is at farthest distance from y− axis at t≥4. Hence the available correct choice is t=4.
Similar Questions
A particle is initially at rest. It starts moving with a constant acceleration, the speed of the particle in t seconds is 50m/s and after one second the speed becomes 75m/s. calculate the acceleration of the particle and distance covered in (t+1)th second of its motion.
View SolutionA particle stats from rest at the origin with a constant acceleration
Calculate the position of the particle at t=5 second.View Solution
Knowledge Check
- Question 1 - Select One
A particle which is initially at rest at the origin, is subjection to an acceleration with x− and y− components as shown. After time t=5 , the particle has no acceleration.

What is the magnitude of velocity of the particle at t=2 seconds ?A10√5m/sB5√10m/sC5√5m/sDNone of these - Question 2 - Select One
A particle which is initially at rest at the origin, is subjection to an acceleration with x− and y− components as shown. After time t=5 , the particle has no acceleration.

What is the magnitude of average velocity of the particle between t=0 and t=4 seconds ?A52√13m/sB52√17m/sC30m/sDNone of these - Question 3 - Select One
A particle initially at rest is subjected to two forces, one is constant, the other is retarding force proportional to the particle velocity. In the subsequent motion of the particle, the acceleration
Awill increases then decreasesBwill decreases than increasesCwill decreases to zeroDwill decrease and become constant at some non zero value.
A particle initially at rest starts moving along x-axis.Its acceleration varies with time as a=6tm/s^(2) .If it starts from x=10m .Then the position of particle at t=2s is
View SolutionDisplacement x versus t2 graph is shown for a particle. The acceleration of particle is
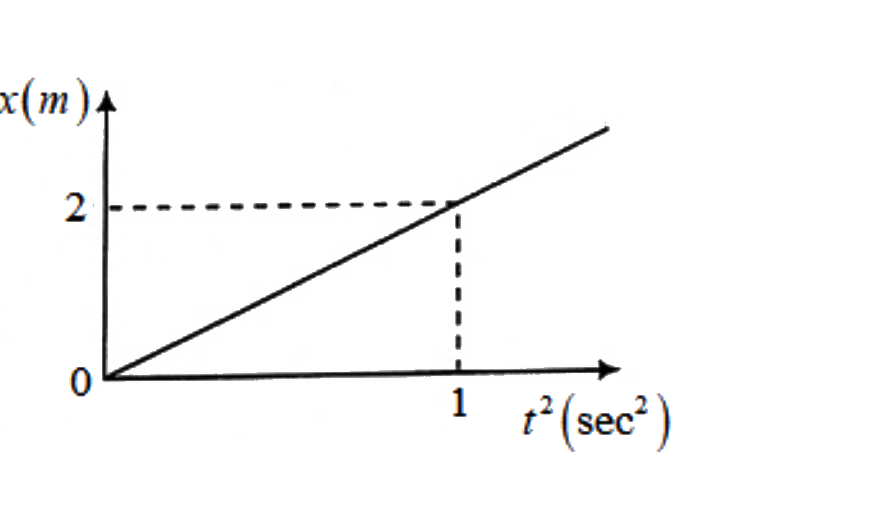 View Solution
View SolutionParticle A starts from rest and moves along a straight line. Acceleration of the particle varies with time as shown in the graph. In 10 s the velocity of the particle becomes 60m/s and the acceleration drops to zero. Another particle B starts from the same location at time t=1.1s and has acceleration – time relationship identical to A with a delay of 1.1s. Find distance between the particles at time t=15s.
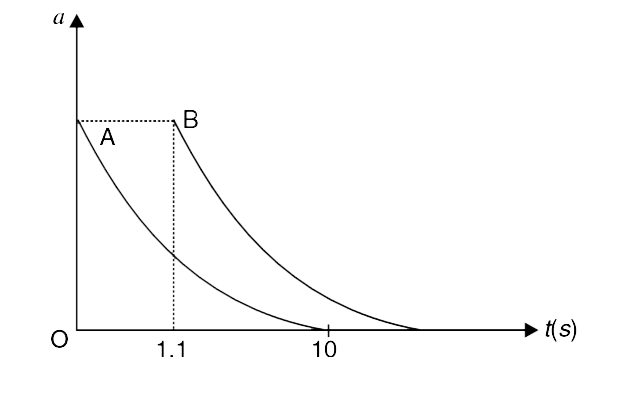 View Solution
View SolutionA particle starts from rest (at x=0) when an acceleration is applied to it. The acceleration of the particle changes with its co-ordinate as shown in the fig. Find the speed of the particle at x=10m.
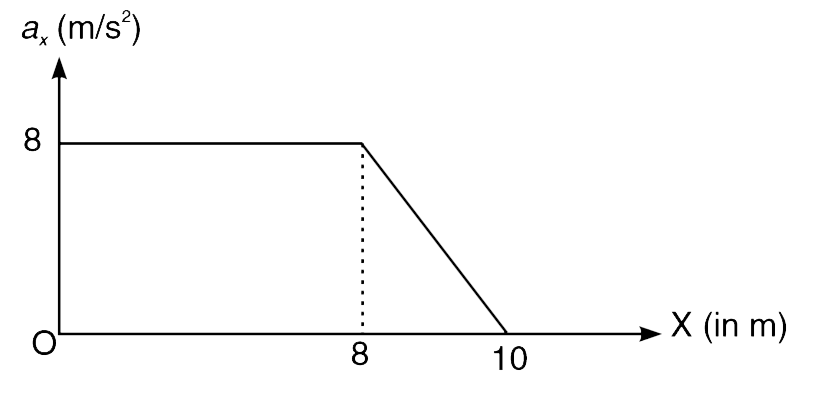 View Solution
View SolutionA particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
View Solution

