A meter stick AB of length 1 meter rests on a frictionless floor in horizontal position with end A attached to the string as shown. Assume that string connecting meter stick with pulley always remains vertical.

Minimum magnitude of relative velocity of A with respect to B during the motino specified in question 5 is :
2m/s
4m/s
6m/s
none of these
The correct Answer is:B
→vA=4ˆjm/s and →vB=(−4tanθˆi)m/s
∴→vAB=(4tanθˆi+4ˆj)m/s
∴vAB=4√1+tan2tan=4cosθ
∴(vAB)min=4m/s
Similar Questions
Two block A and B of masses 1kg and2kg respectively are connected by a string, passing over a light frictionless pulley B as shown. Another string connect the center of pulley. Both the blocks are resting on a horizontal floor and the pulley is help such that string remains just taut. At moment t=0, a force F=20t starts acting on the pully along vertically upwards direction as shown in figure.Calculate

(a) velicity of A when B loses contact with the floor.
(b) height raised by the pulley upto that instant.
(Take =g=10m/s2)View SolutionA rod length AB is moving with ends remaining in contact with frictionless wall and floor . If at the instant shown , the velocity of the and B is 3ms−1 towards the negative x-direction , then the magnitude of the velocity of the end A wll be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
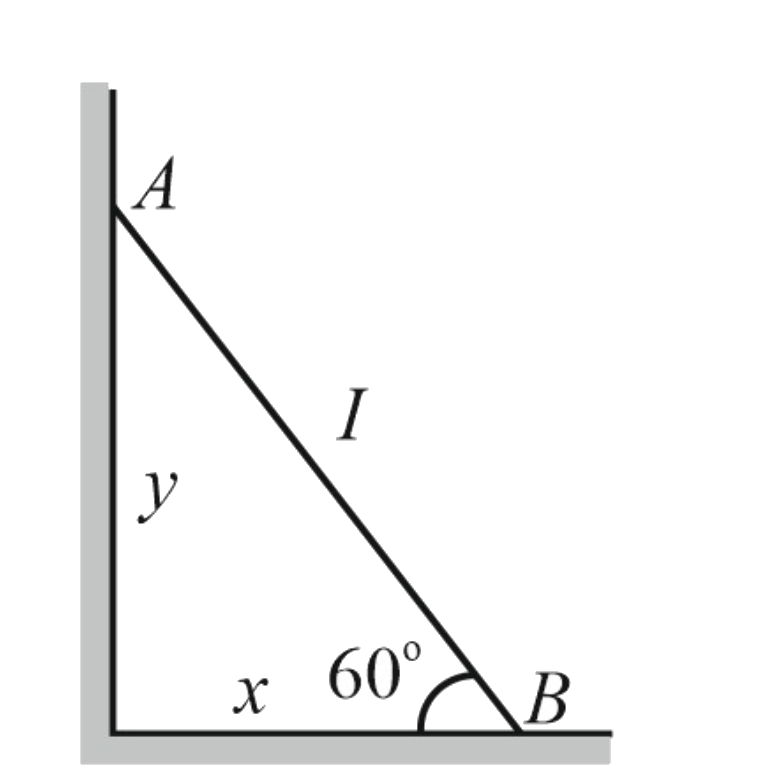
A meter stick AB of length 1 meter rests on a frictionless floor in horizontal position with end A attached to the string as shown. Assume that string connecting meter stick with pulley always remains vertical.

Time taken to cover the distance in above part is :A(√2+14√2)secB(√2−14√2)secC14√2secD18sec - Question 2 - Select One
A meter stick AB of length 1 meter rests on a frictionless floor in horizontal position with end A attached to the string as shown. Assume that string connecting meter stick with pulley always remains vertical.
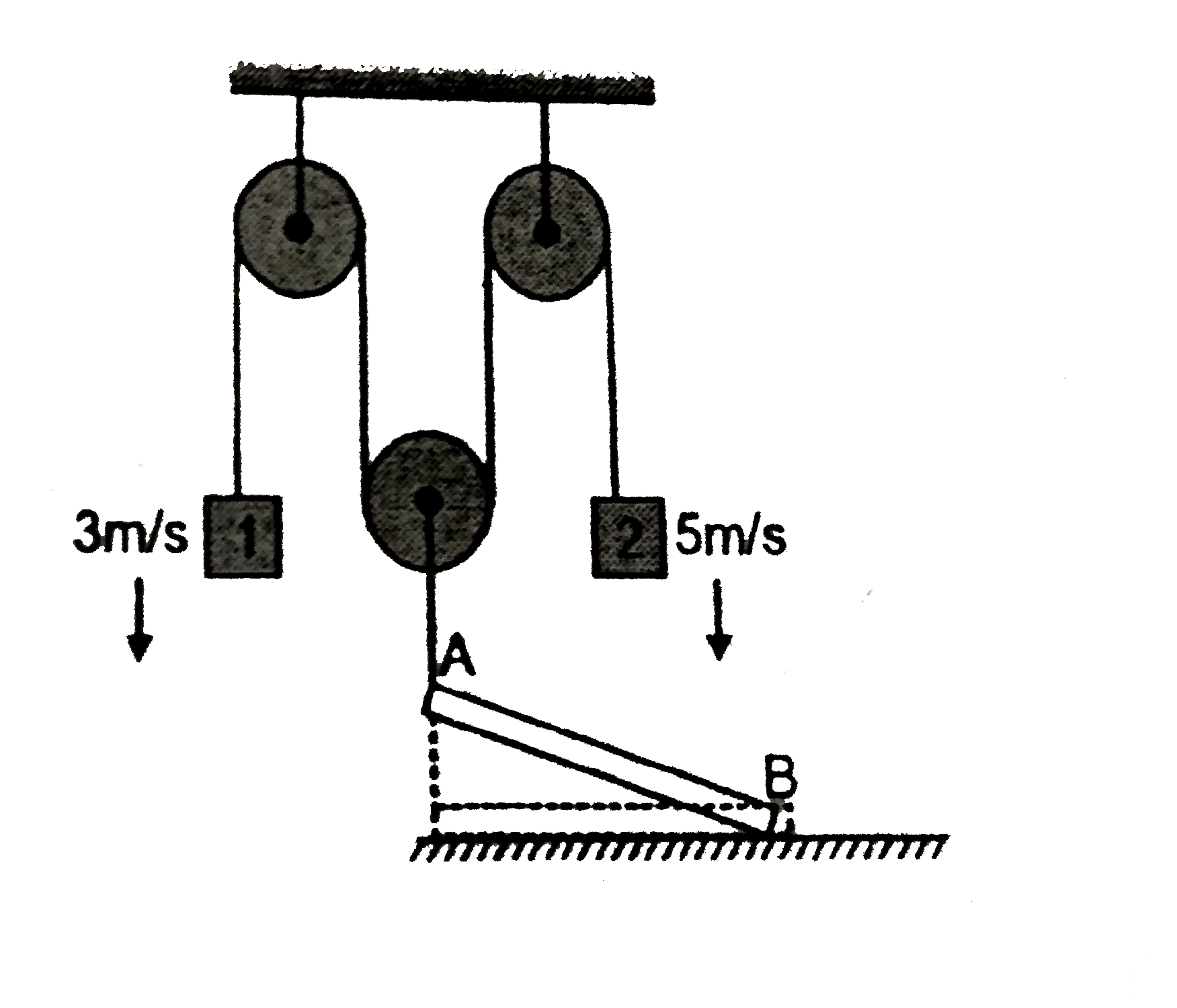
If block 1 and 2 are given constant speeds as shown then the distance moved by end B over the floor in the period for which speed of B is less than A.A(√2+1√2)mB(√2−1√2)mC1√2mD12m - Question 3 - Select One or More
A light stick of length l rests with its one end against the smooth wall and other end against the smooth horizontal floor as shown in the figure. The bug starts at rest from point B and moves such that the stick always remains at rest. aP is the magnitude of acceleration of but of mass m, which depends upon its distance of x from the top end of the stick. Choose the correct option (s)
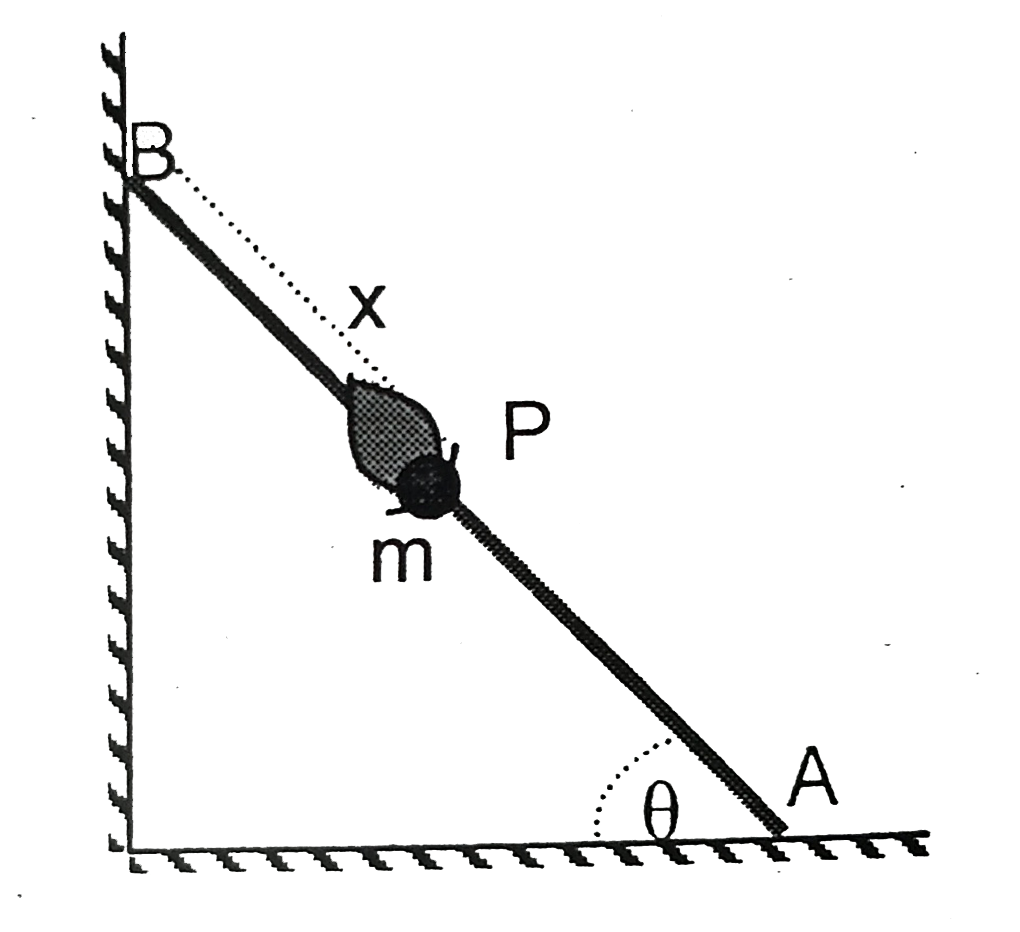 AaP=gsinθ(1−dl)BaP=gcosθ(1−xl)CThe time taken by the but to reach the bottom of the stick having started at the top end from rest is π2√lsinθ3gDThe time taken by the but to reach the bottom of the stick having started at the top end from rest is π2√lsinθ2
AaP=gsinθ(1−dl)BaP=gcosθ(1−xl)CThe time taken by the but to reach the bottom of the stick having started at the top end from rest is π2√lsinθ3gDThe time taken by the but to reach the bottom of the stick having started at the top end from rest is π2√lsinθ2
A stick AB of mass M is tied at one end to a light string OA. A horizontal force F=Mg is applied at end B of the stick and its remains in equilibrium in position shown. Calculate angles α and β.
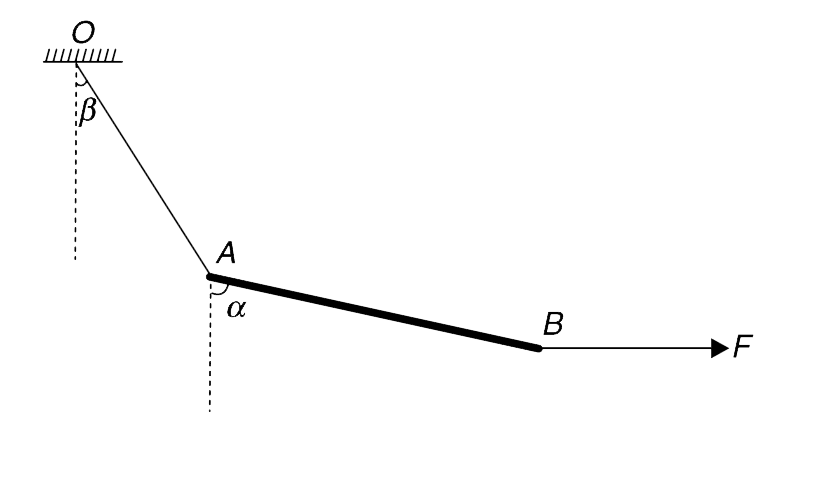 View Solution
View SolutionA stick of length a cm rests against a vertical wall and the horizontal floor. If the foot of thes tick slides with a constant velocity of b cm/s,then the magnitude of the velocity of the middle point of the stick when it is equally inclined with the floor and the wall, is
View SolutionA rod of length 10 meter has one end on smooth floor and the other end on smooth wall is released from the rest the position shown in figure. When the rod makes an angle of 37∘ with the horizontal, answer the following:

The angular velocity of rod is:View SolutionA transerse sinusodial wave of amplitude 2mm is setup in a long uniform string. Snapshot of string from x=0 to x=π meter is taken at t=0, which is shown. Velocity of point P is in −y direrction. Magnitude of relative velocity of P with respect to Q is 2cm/s. Choose the correct options : wave equation is
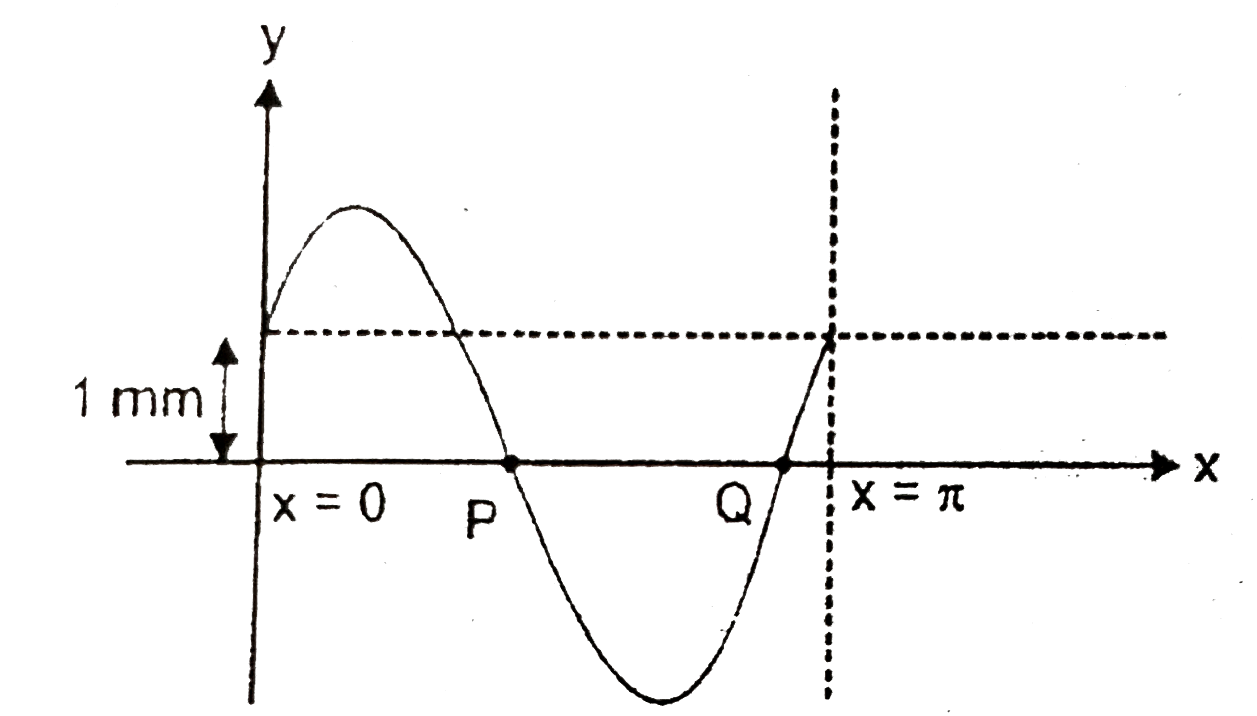 View Solution
View SolutionA rod of length 10 meter has one end on smooth floor and the other end on smooth wall is released from the rest the position shown in figure. When the rod makes an angle of 37∘ with the horizontal, answer the following:

The velocity of centre of mass of rod is :View Solution

