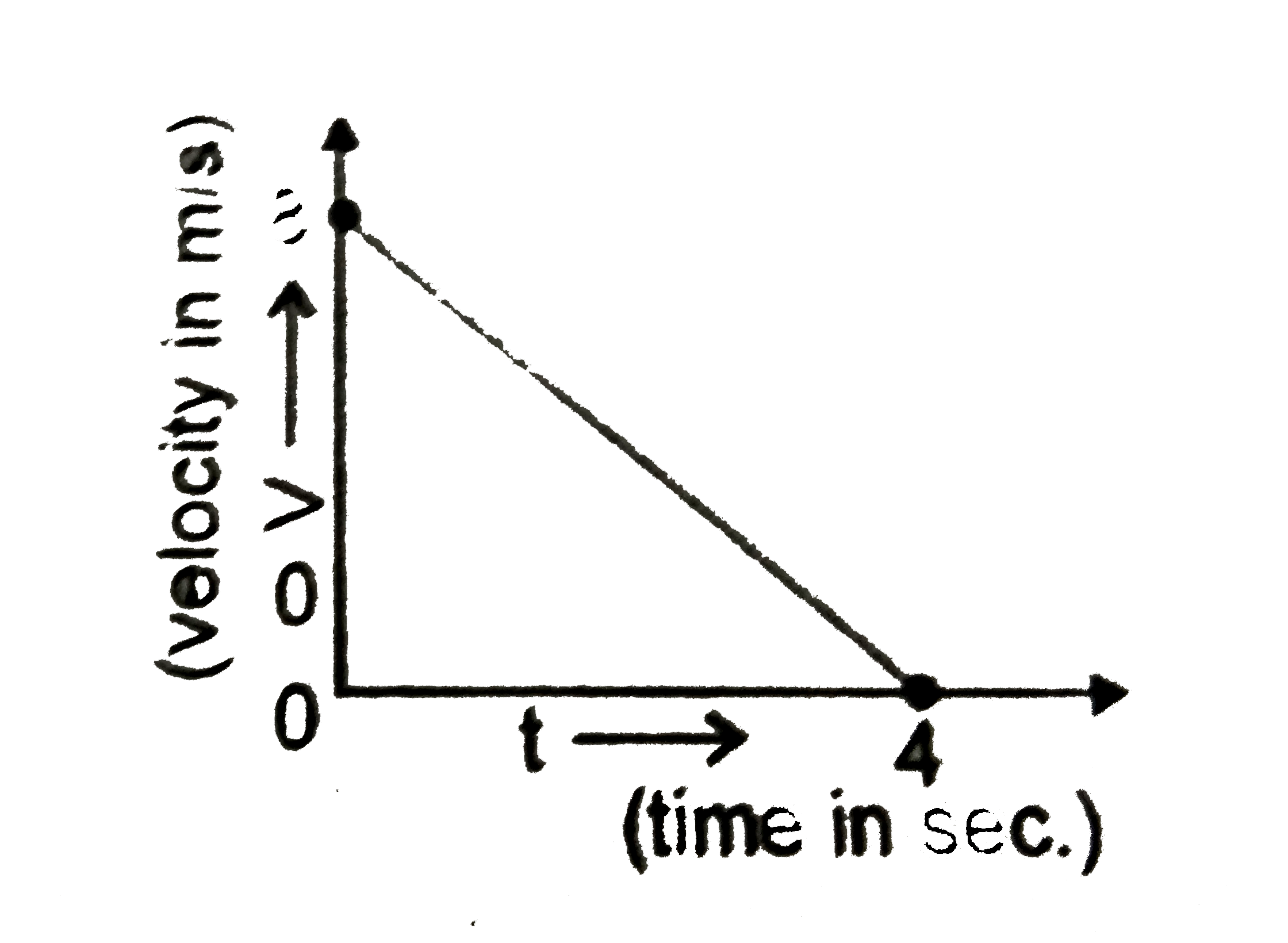
A block of mass 2kg is given a push for a moment horizontally and then the block starts sliding over a horizontal plane. The graph shows the velocity− time of the motion. The co− efficient of sliding friction between the plane and the block is :
0.02
0.20
0.04
0.40
The correct Answer is:B
The magnitude of declaration from graph is
a=8−04−0=2m/s2
The declaration of block is
a=μg∴Mu=ag=0.2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 32
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 33
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Comprehension
127 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Block of mass 10 kg is moving on inclined plane with constant velocity 10 m/s. The coedfficient of kinetic friction between incline plane and block is :-

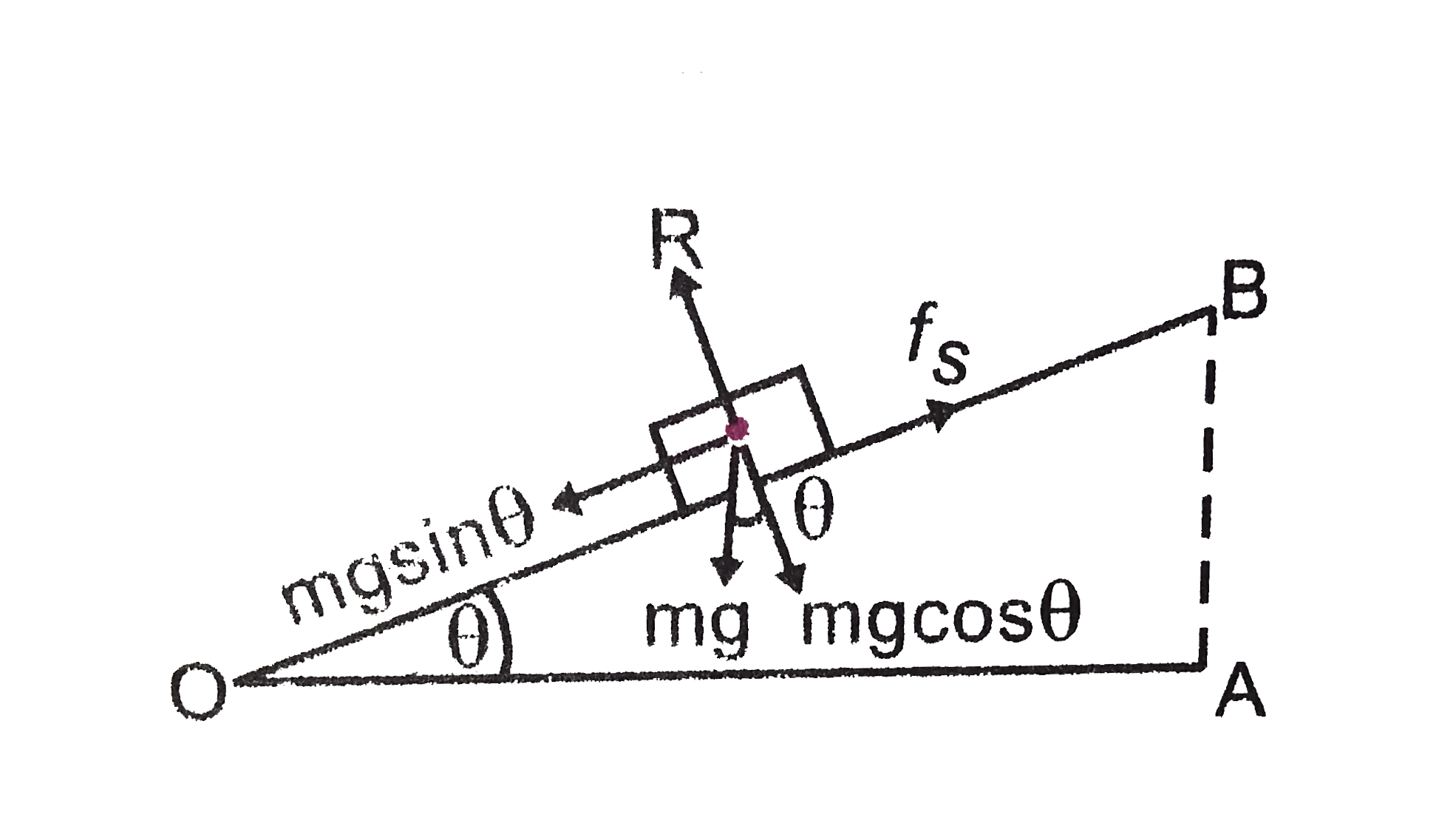
View SolutionA mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
View Solution
Knowledge Check
A block is sliding on a rough horizontal surface. If the contact force on the block is √2 times the frictional force, the coefficient of friction is
A0.25B1√2C√2D1A block B is pushed momentarily along a horizontal surface with an initial velocity v. If μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time
 AvgμBgμvCgvDvg
AvgμBgμvCgvDvgA block B is pushed momentarily along a horizontal surface with an initial velocity v. If μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time
 AvgμBgμvCgvDvg
AvgμBgμvCgvDvg
A small block of mass 'm' is placed on a plank of mass 'M'. The block is connected to plank with the help of a light string passing over a light smooth pulley as shown in figure. The co-efficient of static friction between the block and plank is μ.
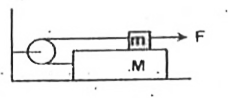
The co-efficient of friction between the plank and the horizontal surface is zero. What maximum horizontal force F applied on the block of mass m can make the block and plank not to slide relatively?
View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If mu is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:

View SolutionA block sliding down on a rough 45∘ inclined plane has half the velocity it would have been, the inclined plane is smooth. The coefficient of sliding friction between the block and the inclined plane is
View SolutionA block sliding down on a rough 45∘ inclined planes has half the velocity it would have been, the inclined plane is smooth. The coefficient of sliding friction between the the block and the inclined plane is
View SolutionA block of mass 4kg rests on a rough horizontal plane. The plane is gradually inclined until at an angle θ=60∘ , with the vertical, the mass just begins to side. What is the coefficient of static friction between the block and the plane?
View Solution
