Two blocks of mass 10kg and 2kg respectively are connected by an ideal string passing over a fixed smooth pulley as shown in figure. A monkey of mass 8kg started climbing the string with a constant acceleration of 2m/s2 with respect to string at t=0 . Initially the system is in equilibrium and monkey is at a distance 2.4 from the pulley. Find the time taken by monkey to reach the pulley in sec.
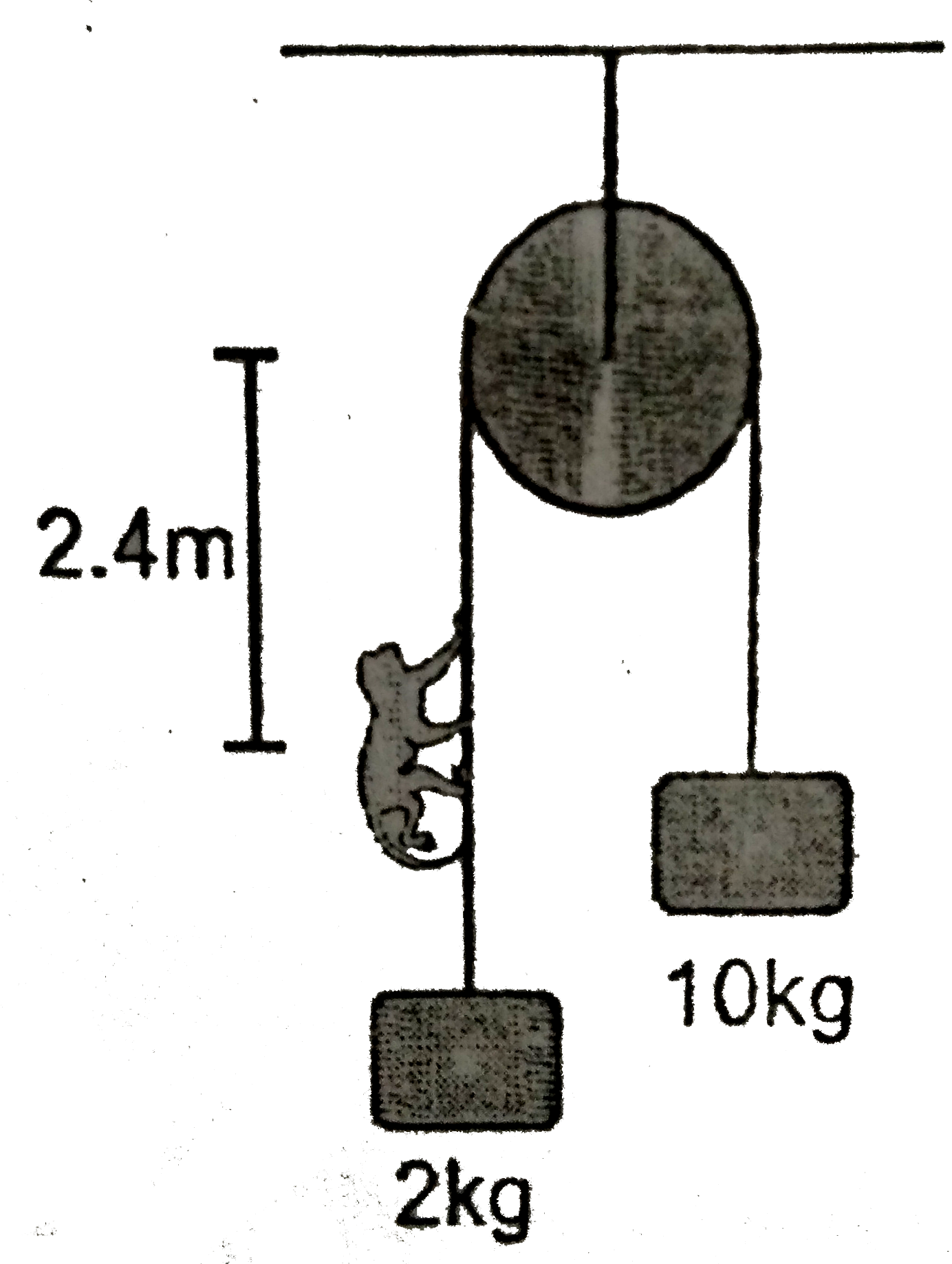
The correct Answer is:2sec.
a(cm)left=acm
8(a0−a)−2a8+2=10a10
a=25a0

am=a0−a=35a0=1.2m/s2
t=√2×Sam=2Sec.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 365videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Dpp 378videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 345videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
Two masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
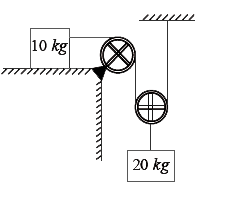 View Solution
View SolutionTwo bodies of masses 4kg and 3kg respectively are connected by a light string passing over a smooth frictionless pulley Calculate the acceleration of the masses and tension in the string .
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of mass 10kg and 2kg respectively are connected by an ideal string passing over a fixed smooth pulley as shown in figure. A monkey of 8kg started climbing the string with constant acceleration 2ms−2 with respect to string at t=0. Initially the monkey is 2.4m from the pulley. Find the time taken by the monkey to reach the pulley.
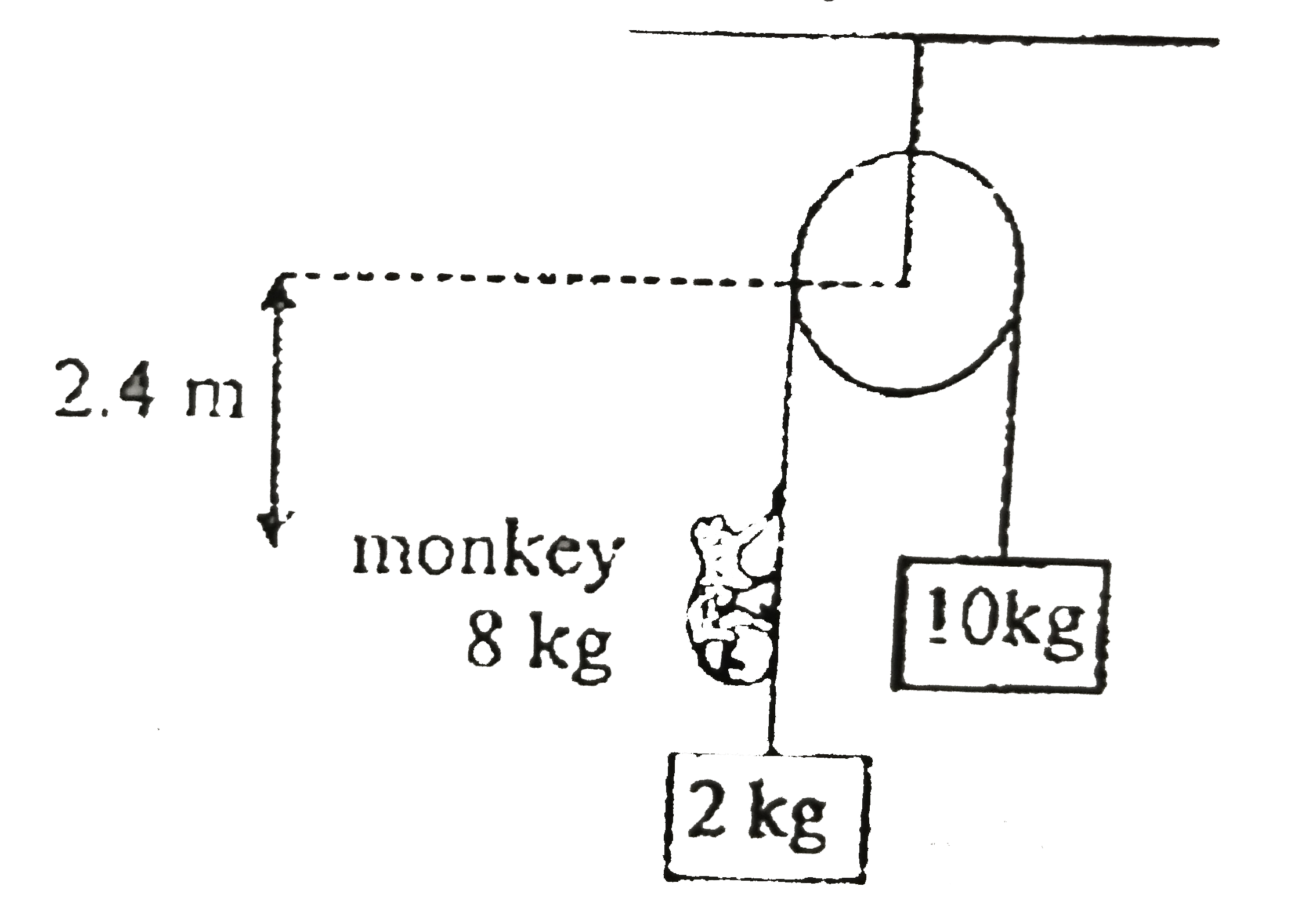 A1 secB2 secC4 secD8 sec
A1 secB2 secC4 secD8 sec - Question 2 - Select One
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2 - Question 3 - Select One
Two blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is
 A50N up the planeB50N down the planeC100N up the planeD100N down the plane
A50N up the planeB50N down the planeC100N up the planeD100N down the plane
Two unequal masses of 1kg and 2kg are connected by an inextensible light string passing over a smooth pulley as shown in figure. A force F=20N is applied on 1kg block find the acceleration of either block (g=10m/s2).
 View Solution
View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 View Solution
View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 View Solution
View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
 View Solution
View SolutionTwo Block A and B of masses 10kg and 6kg respectively are connected through pulley as shown in figure. Find acceleration of block A.
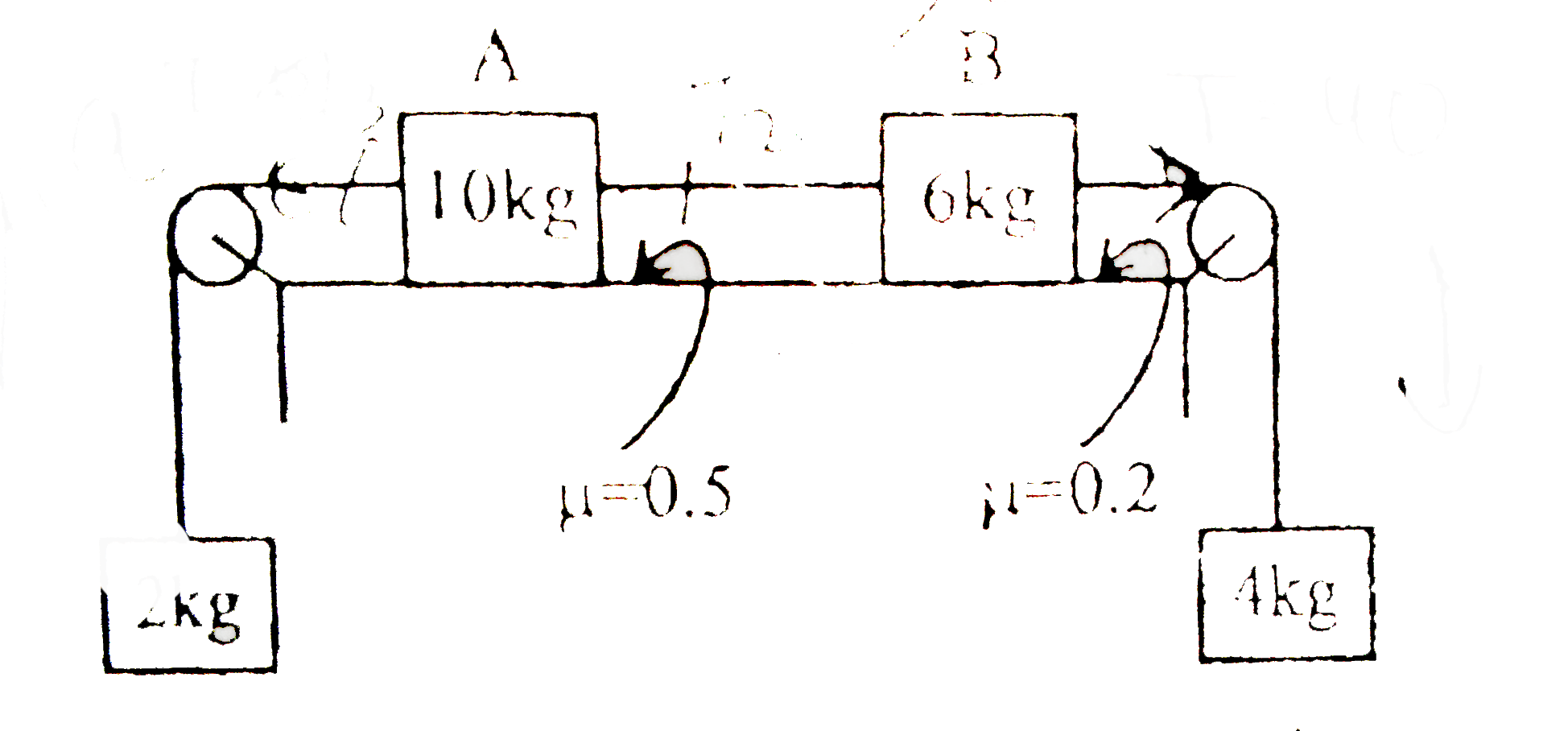 View Solution
View Solution

