A block of mass m is placed on a rough inclined plane. The coefficient of friction between the block and the plane is μ and the inclination of the plane is θ. Initially theat−0 and the block will certain stationary on the plane. Now the inclination θ is gradually increased. The block presses the inclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the block starts sliding, the angle θ for which the block starts sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction ( frictional force) and the shear reaction (frictional force) . The net contact force will be resultant of both.

If the entire system, were accelerated upward with acceleration 'a', the angle of repose , would :
increases
decreases
remain same
increase of a>g
The correct Answer is:C
Angle (θ') fo repose :
m(g+a)sinθ'=F
m(g+a)cosθ'=R
∴FR=tanθ'
θ'=tan−1(FR)=α
Hence angle of repose does not change.
Similar Questions
क्षैतिज से θ कोण पर झुके आनत तल पर m द्रव्यमान का गुटका रखा है । गुटके तथा आनत तल के बीच घर्षण गुणांक μ है । गुटके पर लगने वाला घर्षण बल है -
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA body is placed on a rough inclined plane of inclination θ. As the angle θ to 90∘ the contact force between the block and the plane
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block with a square base measuring a×a and height h, is placed on an inclined plane. The coefficient of friction is μ. The angle of inclination (θ) of the plane is gradually increased. The block will
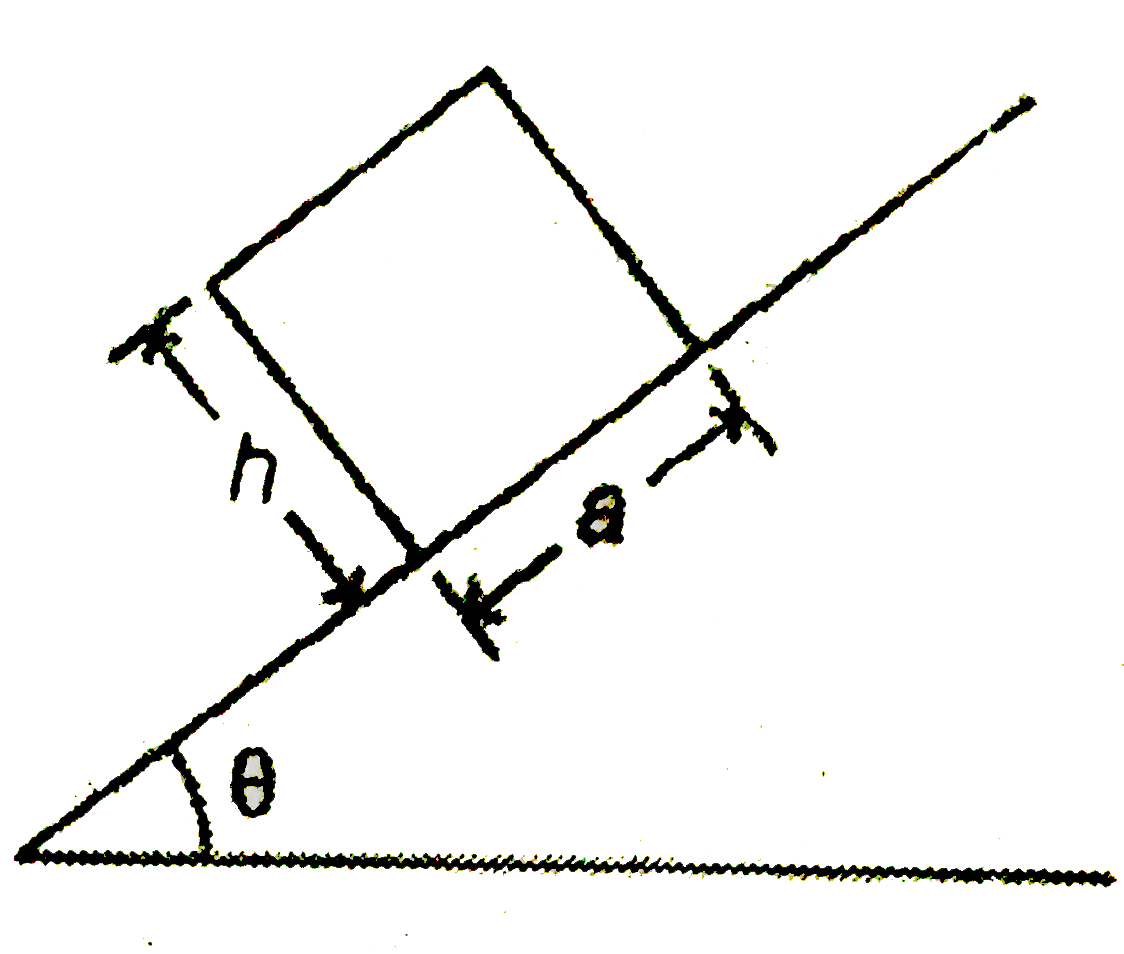
View SolutionA block of mass m slides down an inclined plane of inclination theta with uniform speed. The coefficient of friction between the block and the plane is mu . The contact force between the block and the plane is
View Solution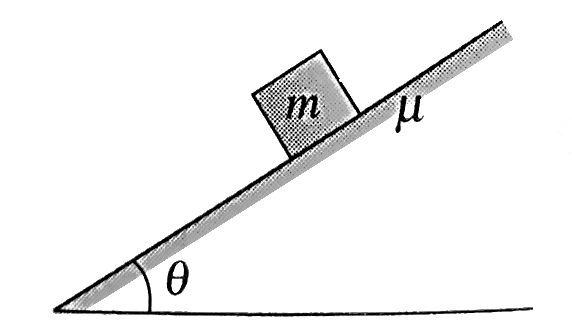 A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is μ and the inclination of the plane is θ.Initially θ=0 and the block will remain stationary on the plane. Now the inclination θ is gradually increased . The block presses theinclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle θ for which the block start sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. For what value of θ will the block slide on the inclined plane:
View Solution
