The blocks ov mass m1kg and m2=2kg are connected by an ideal spring, rest on a rough horizontal surface. The spring is unstressed. The spring constant of spring is K=2N/m. The coefficient of friction between blocks and horizontal surface is μ=12. Now the left block is imparted a velocity u towards right as shown. The largest value of u( in m/s) such that the block of mass m2 never moves is ( Take g=10m/s2)
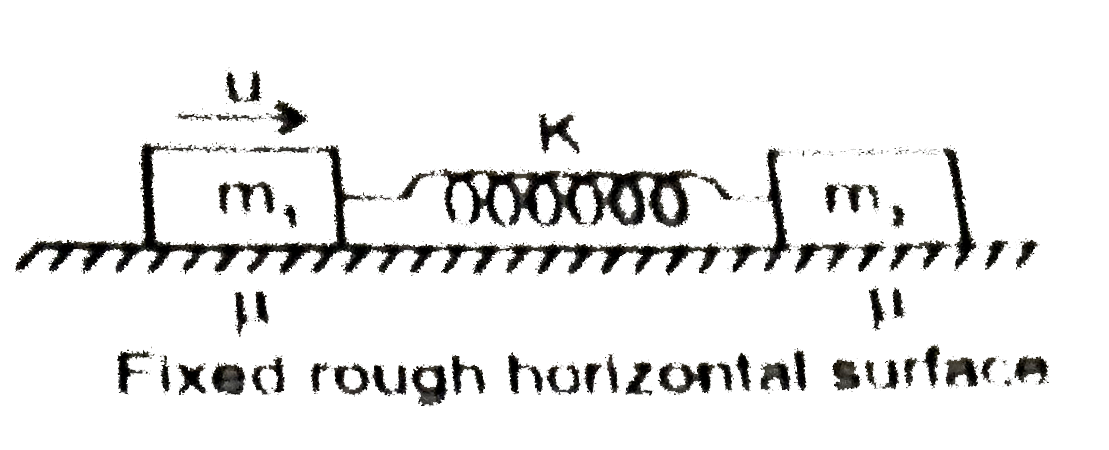
The correct Answer is:1−m/s
For the block of mass m2, not to move, the maximum compression in the spring x0 should be such that
kx0=μm2g…..(1)
Applying work energy theorem to block of mass m1 we get
12m1u2=12μ2m22g2K+μ2+m1m2g2K putting the appropriate value we get u=10m/s.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 39
3 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 40
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - Dpp 37
8 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Two blocks of masses m1=10kg and m2=20kg are connected by a spring of stiffness k = 200 N/m. The coefficient of friction between the blocks and the fixed horizontal surface is μ=0.1. Find the minimum constant horizontal force F (in Newton) to be applied to m1 in order to slide the mass m2. (Take g=10m/s2)
View SolutionTwo blocks of Masses M and 2M are connected by a spring of stiffness k .The coefficient of friction between the blocks and the surface is mu Find the minimum constant force F to be applied to 2m in order to slide the mass M .
View Solution
Knowledge Check
Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separatelyBthe magnitude of momentums of each body are equal to each otherCthe mechanical energy of system remains constantDboth (C) and (B) are correctTwo blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
AF=μ(m1+m22)gBF=μ(m12+m2)gCF=μ(m21+m222)gDF=μ2(m21+m22)gTwo block of same mass'm' are joined with an dideal spring of spring constant k and sept on a rough surface as shown in figure. The spring is initially unstretched and coefficient of friction between the blocks and horizontal surface is μ and 2μ respectively. What should be the maximum speed of block 'A' such that the block 'B' does not move ?
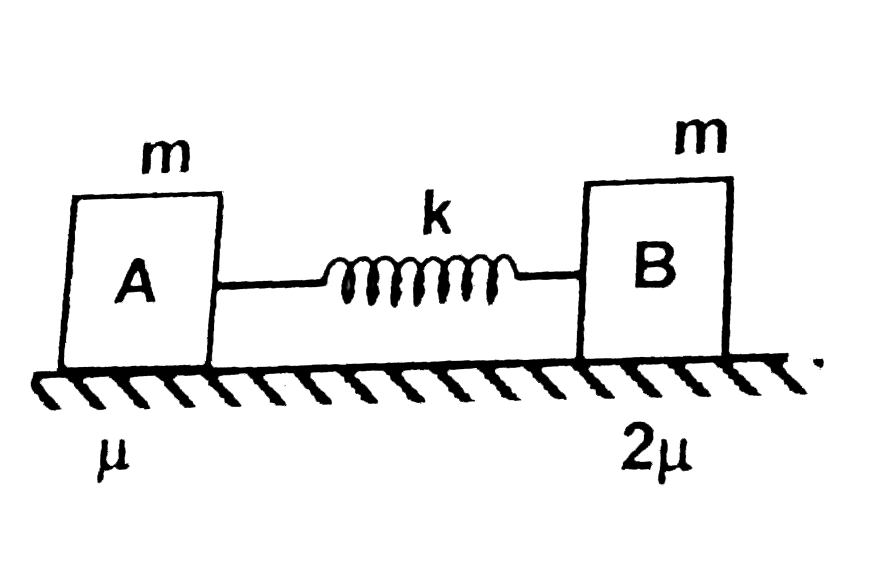 A2μg√2mkBμg√2mkCμg√mkD2μg√m2k
A2μg√2mkBμg√2mkCμg√mkD2μg√m2k
Two block of masses m1 and m2 connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1 in order to shift the other block?
View SolutionA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is

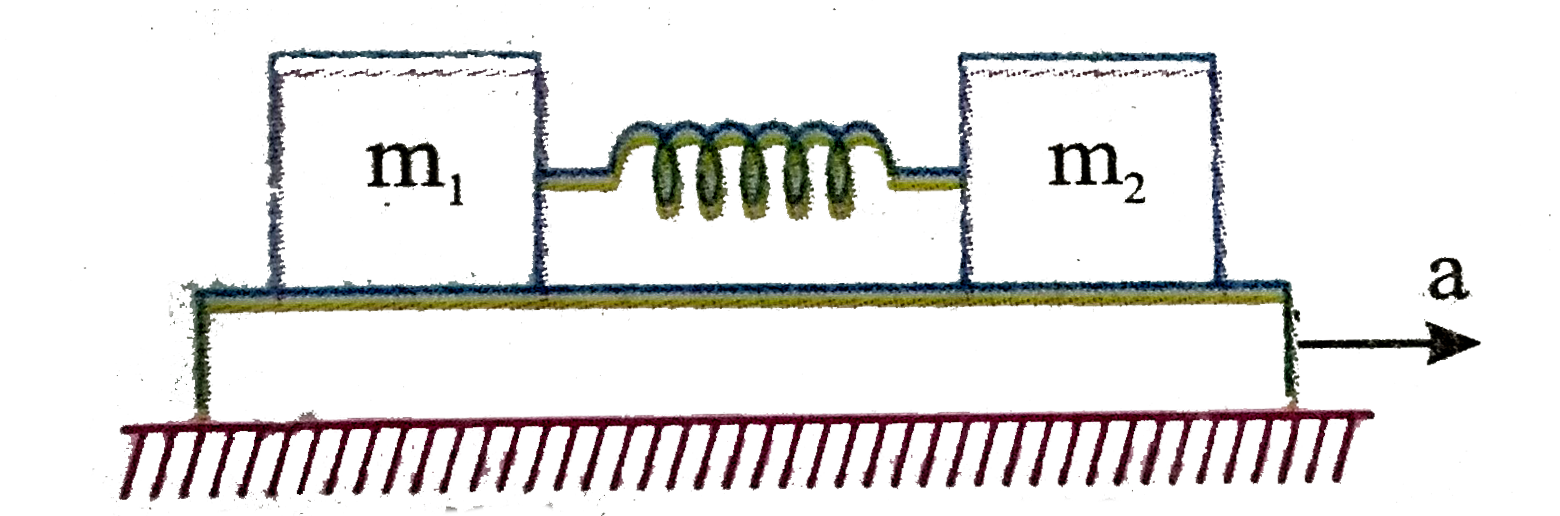
View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
View SolutionTwo blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of osciallation is
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
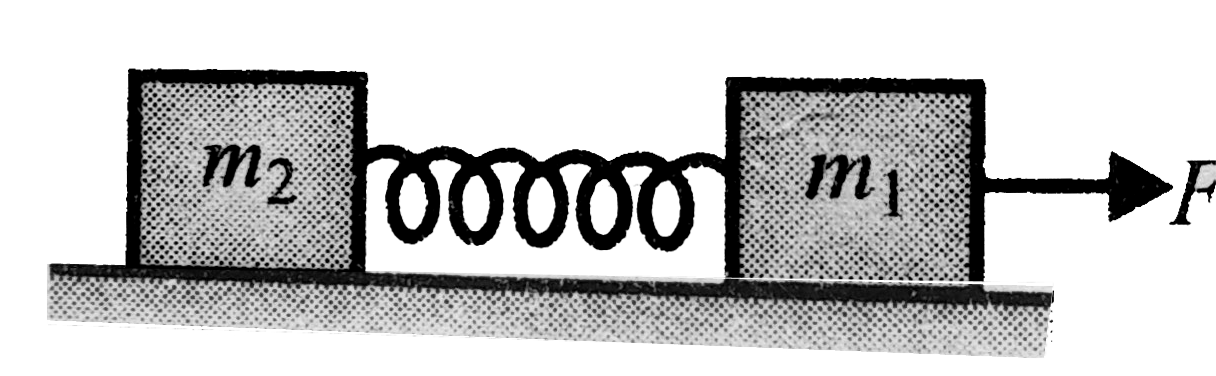
What is maximum elongation of spring.
View Solution
