A particle of mass 'm' moves along the quarter section of the circular path whose centre is at the origin . The radius of the circular path is 'a'. A force →F=yˆi−xˆj newton acts on the particle, where x,y denote the coordinates of position of the particle. Calculate the work done by this force in taking, the particle from point, A(a,0) to point B(0,a) along the circular path.
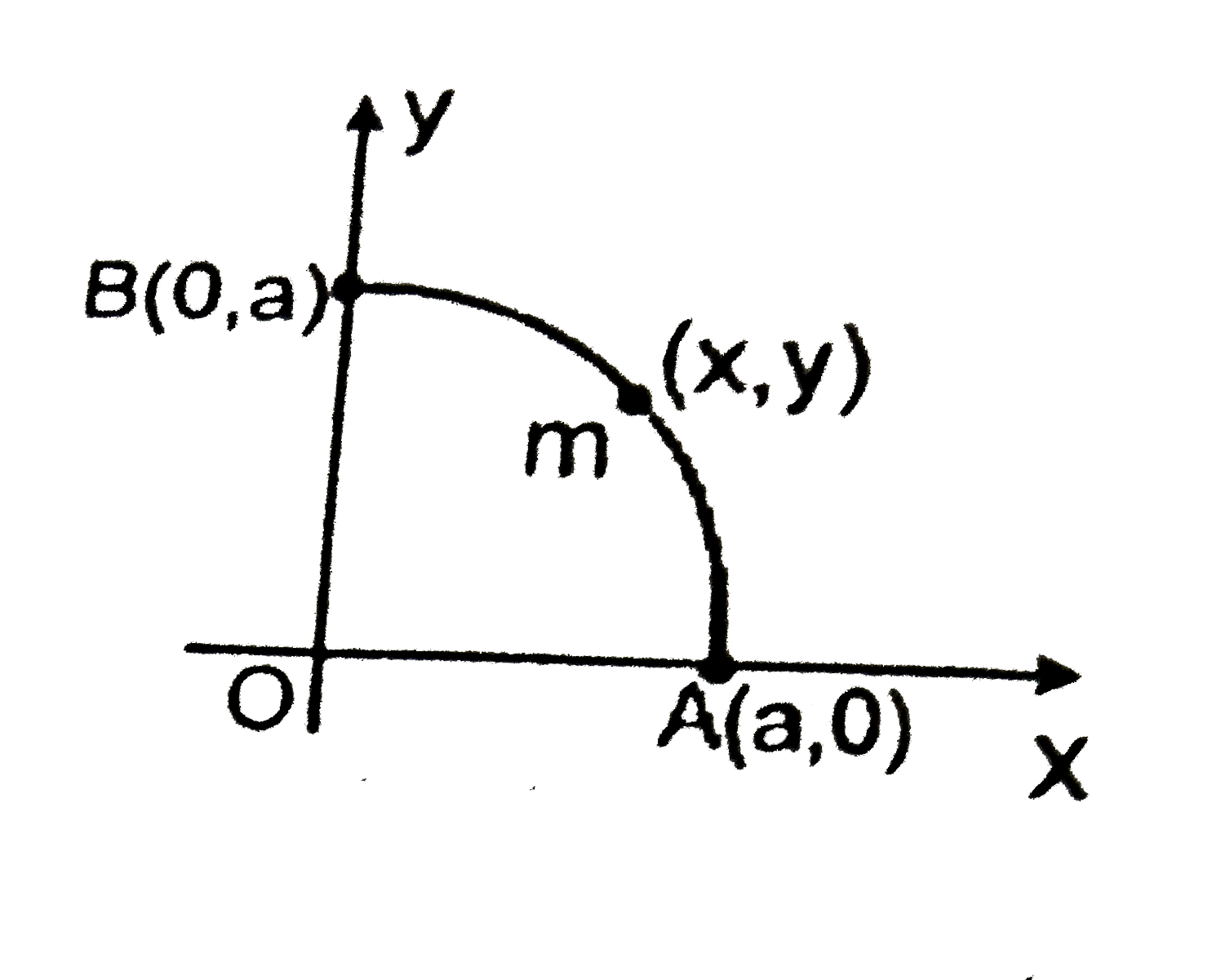
The correct Answer is:−πa22
Work done by force F,
w=∫→F.d→r=∫(yˆi−xˆj).(dxˆi+dyˆj)
∴x2+y2=a2∴xdx+ydy=0
⇒W=∫(y(−ydyx)−xdy)
−∫(x2+y2)xdy
=−∫a0a2√a2−y2dy=−πa22
Aternate Method
It can be observed that the force is tangent to the curve at each point and the magnitude is constant. The direction of force is opposite to the direction of motion of the particle.
∴ work done =(force) × (distance)
=−√x2+y2πa2=−a×πa2=−πa22J
Ans. w=−πa22J
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 40
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 41
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 38
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Force acting on a particle varies with x as shown in figure. Calculate the work done by the force as the particle moves from x = 0 to x = 6.0 m.
View SolutionA particle moving along the circular path with a speed v and its speed increases by g in one second.If the radius of the circular path be r ,then the net acceleration of the particle is?
View Solution
Knowledge Check
A particle moving along the circular path with a speed v and its speed increases by g in one second. If the radius of the circular path be r, then the net acceleration of the particle is:
Av2r+gBv2r2+g2C[v4r2+g2]1/2D[v2r+g]1/2A particle of mass 'm' moves with a constant speed along a circular path of radius r under the action of a force F .Its speed is given by
A√FrmB√FmrC√FrD√FmrA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
A√rFmB√FrC√FmrD√Fmr
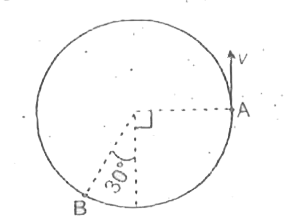
A particle of mass m moves with constant speed v on a circular path of radius r as shown in figure. The average force on it during its motion from A to B is
View SolutionThe force is ………. if the work done by the force in displacing a particle from one point to another is independent of the path followed by the particle .
View SolutionA particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B

View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionA force F=20+10y acts on a particle in y-direction where F is in Newton and y in meter. Wrok done by this force to move the particle from y=0 to y=1m is:
View Solution
