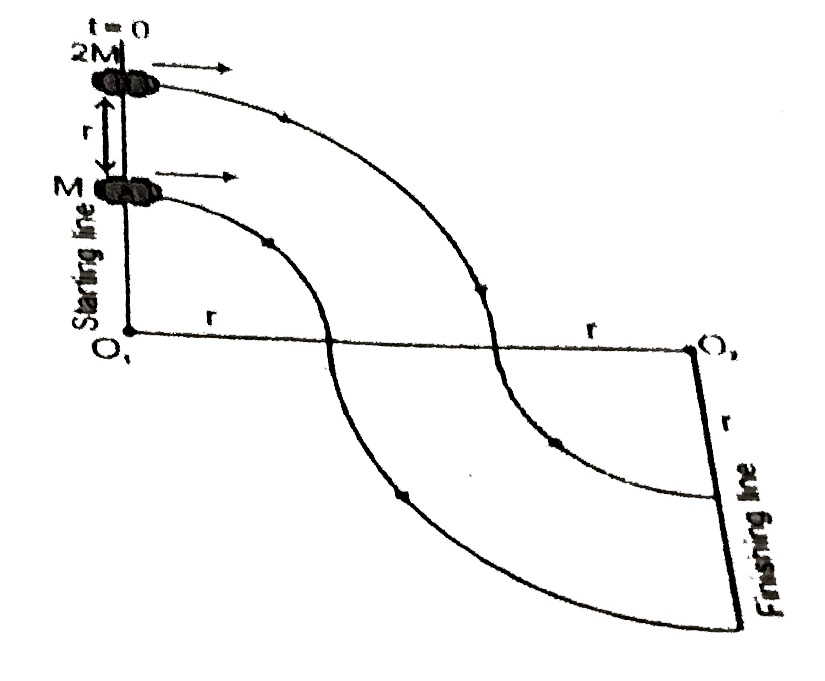
Two racing cars 'A' and 'B' having masses 'M' and '2m' respectively start running from the starting line on a horizontal plane.Both cars 'A' and B' have same speed 'V' which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres O1 and O2 as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.
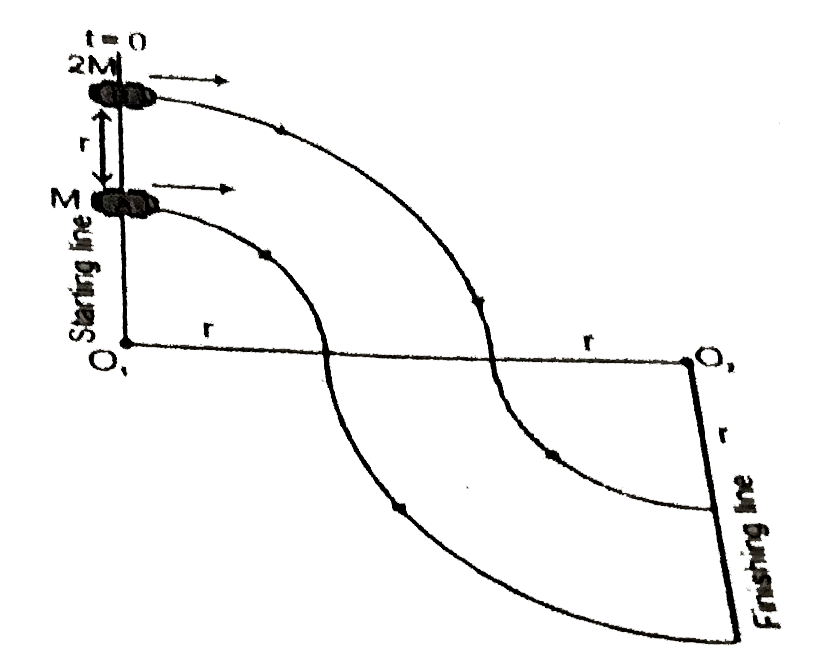
The time interval during which the two cars have same angular speed :
Always along the motion
Never
πr2V
πr4V
The correct Answer is:C
For same angular speed ω
w=2πnt1
n: fractional revelutinar number of revolution
For 'A'n=1/4
w=2π(1/4)t1,w=(vr)
vr=π2t1......(i)
For B car t1=(πr2v)
w=2πrt2=(π4t2)=(v2r)
vr=(π2t2) So time interval for equal angular velocity
⇒Δt=(πr2v)=t1=t2.
Similar Questions
A car goes on a horizontal circular road of radius R. The speed of car is increasing at constant rate a m/s2. If the friction coefficient between the road and the tyre is μ, then the limiting speed of car is
View SolutionA car starts rest, on a horizontal circular road of radius R, the tangential acceleration of the car is a. The friction coefficient between the road and the tyre is μ Find the speed at which car will skid and also find the distance after travelling it skids.
View Solution
Knowledge Check
- Question 1 - Select One
Two racing cars 'A' and 'B' having masses 'M' and '2m' respectively start running from the starting line on a horizontal plane.Both cars 'A' and B' have same speed 'V' which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres O1 and O2 as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.
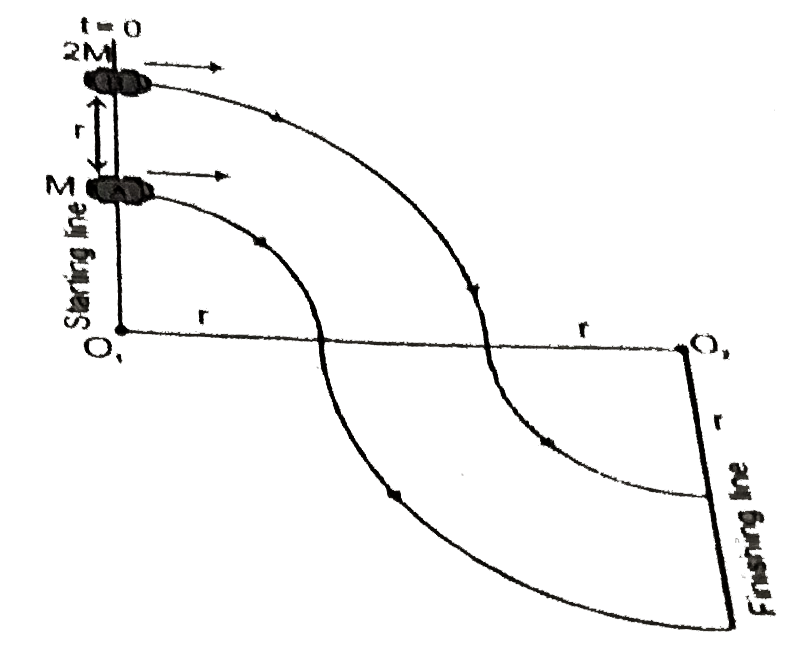
Graph between the magnitude of relative velocity of the two car and time is :A B
B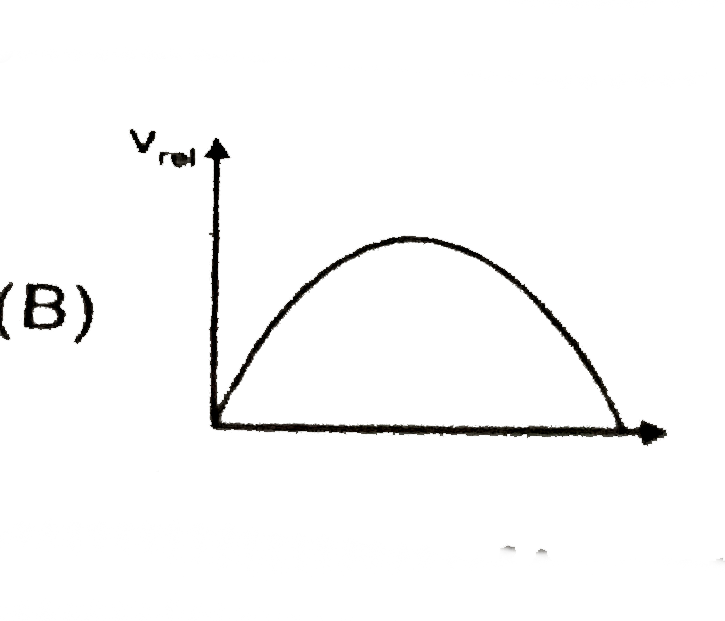 C
C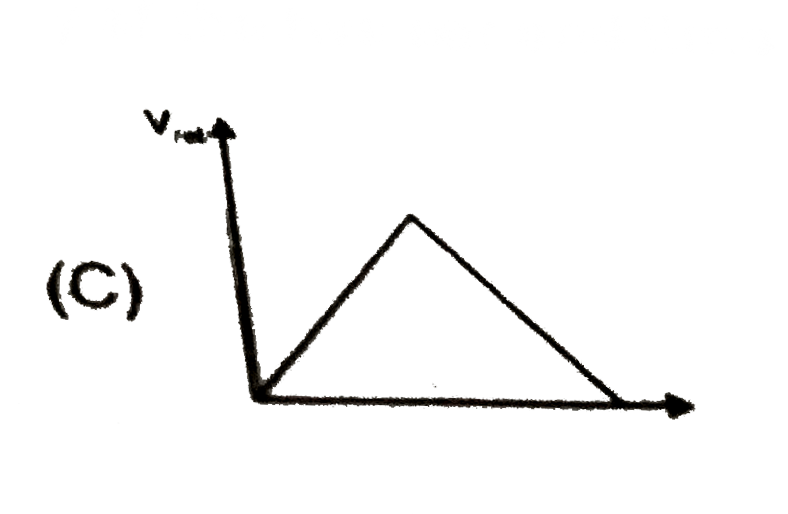 D
D
- Question 2 - Select One
Two racing cars 'A' and 'B' having masses 'M' and '2m' respectively start running from the starting line on a horizontal plane.Both cars 'A' and B' have same speed 'V' which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres O1 and O2 as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.
The magnitude of relative acceleration of two cars when car 'A' just reaches the end of circular arc of radius Y.A0B(√5−2)V22rC√2V2rDV2r - Question 3 - Select One
Two cars, A and B, take the same time to go round around two concentric circular tracks of radii r1andr2, respectively. If r2=4r1, the ratio of the angular speed of car A to that of car B is
A4B14C2D1
Two cars A and B are moving on the straigh parallel paths with speeds 36kmh−1 respectively starting from the same point in the same direction. After 20min, how much behind is car A and from car B?
View SolutionTwo racing cars having masses m1 and m2 move in concentric circles of radius r1 and r2 respectively . If their angular speeds are same , then the ration of their linear speeds is
View SolutionTwo racing cars of masses m1 and m2 are moving in circles of radii r1 and r2 respectively. Their speeds are such that each makes a complete circle in the same duration of time t. The ratio of the angular speed of the first to the second car is
View SolutionTwo cars A and B have masses mAandmB respectively, with mA>mB. Both the cars are moving in the same direction with equal kinetic energy. If equal braking force is applied on both, then before coming to rest
View SolutionA car turns a corner on a slippery road at a constant speed of 10m/s . If the coefficient of friction is 0.5, the minimum radius of the arc in meter in which the car turns is
View Solution

