A uniform circular chain of radius r and mass m rests over a sphere of radius R as shown in figure. Friction is absent everywhere and system is in equilibrium . Find the tension in the chain.
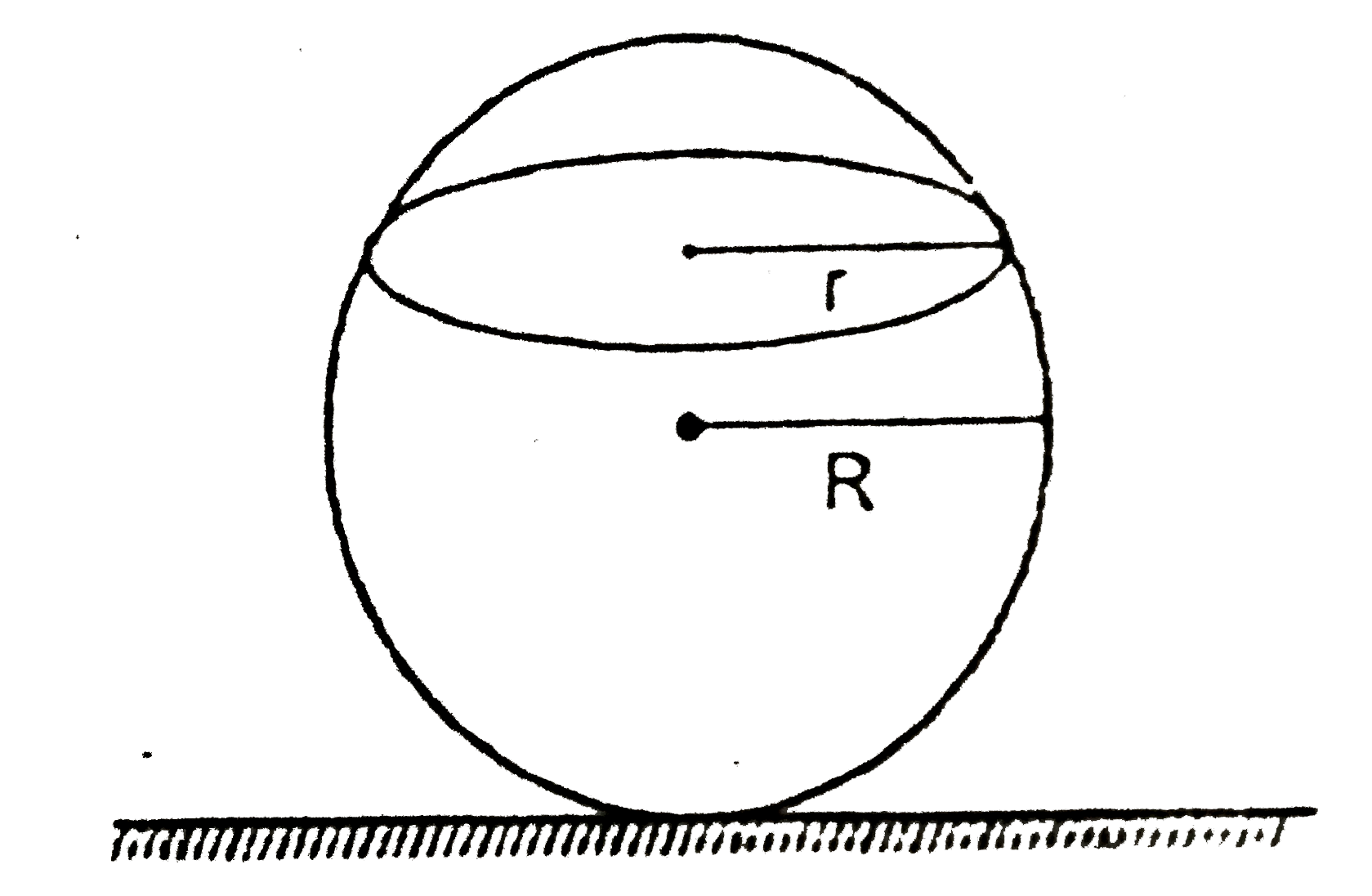
The correct Answer is:T=mg2πr√R2−r2
Consider the dm mass of chain subtending angle at dapha centre
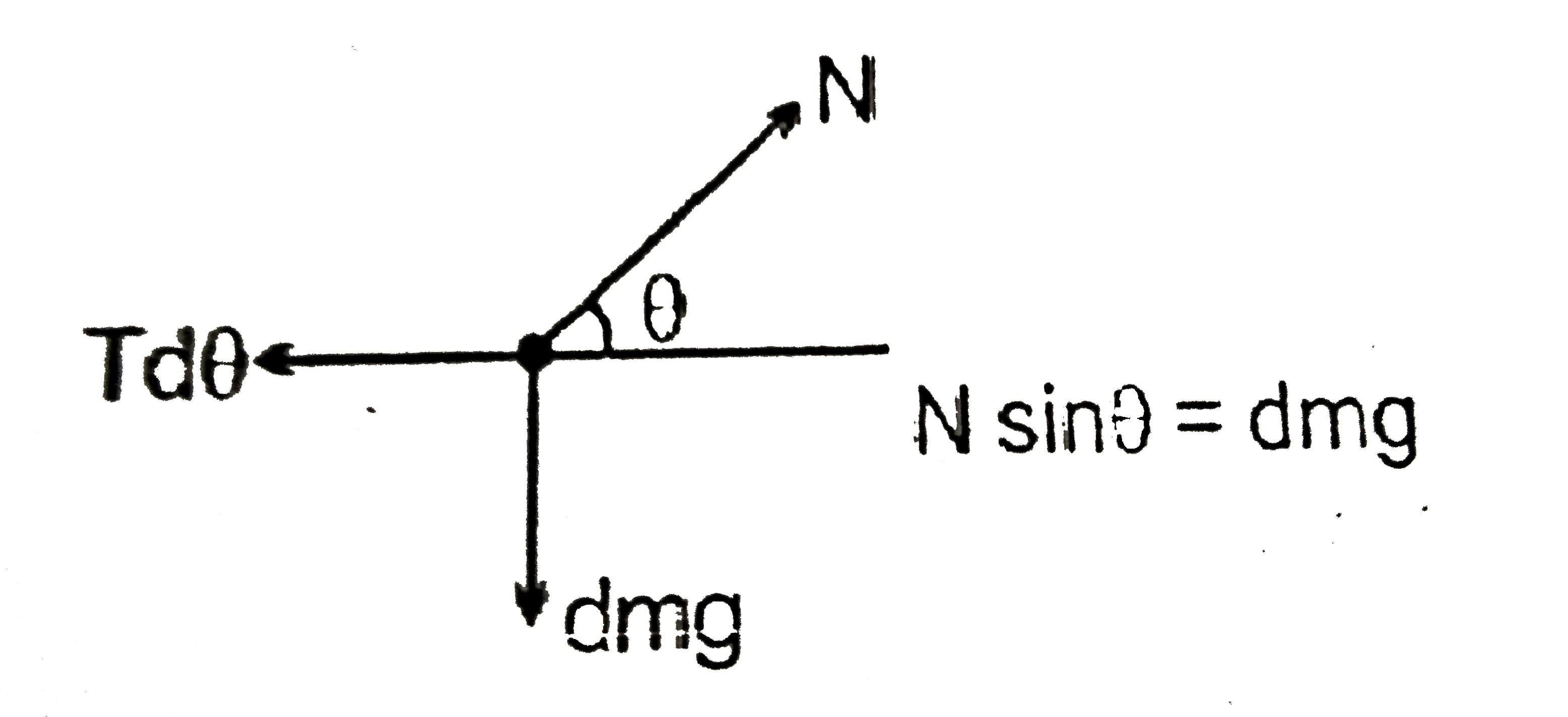
Ncosθ=dmdα.gT
tanθ=m2π.gT,tanθ=√R2−r2r=m2πgT
T=mg2πr√R2−r2Ans.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 58
9 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 59
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 56
7 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Knowledge Check
The semi circular ring of radius R and mass m is free to rotate about the point O in shown figure.
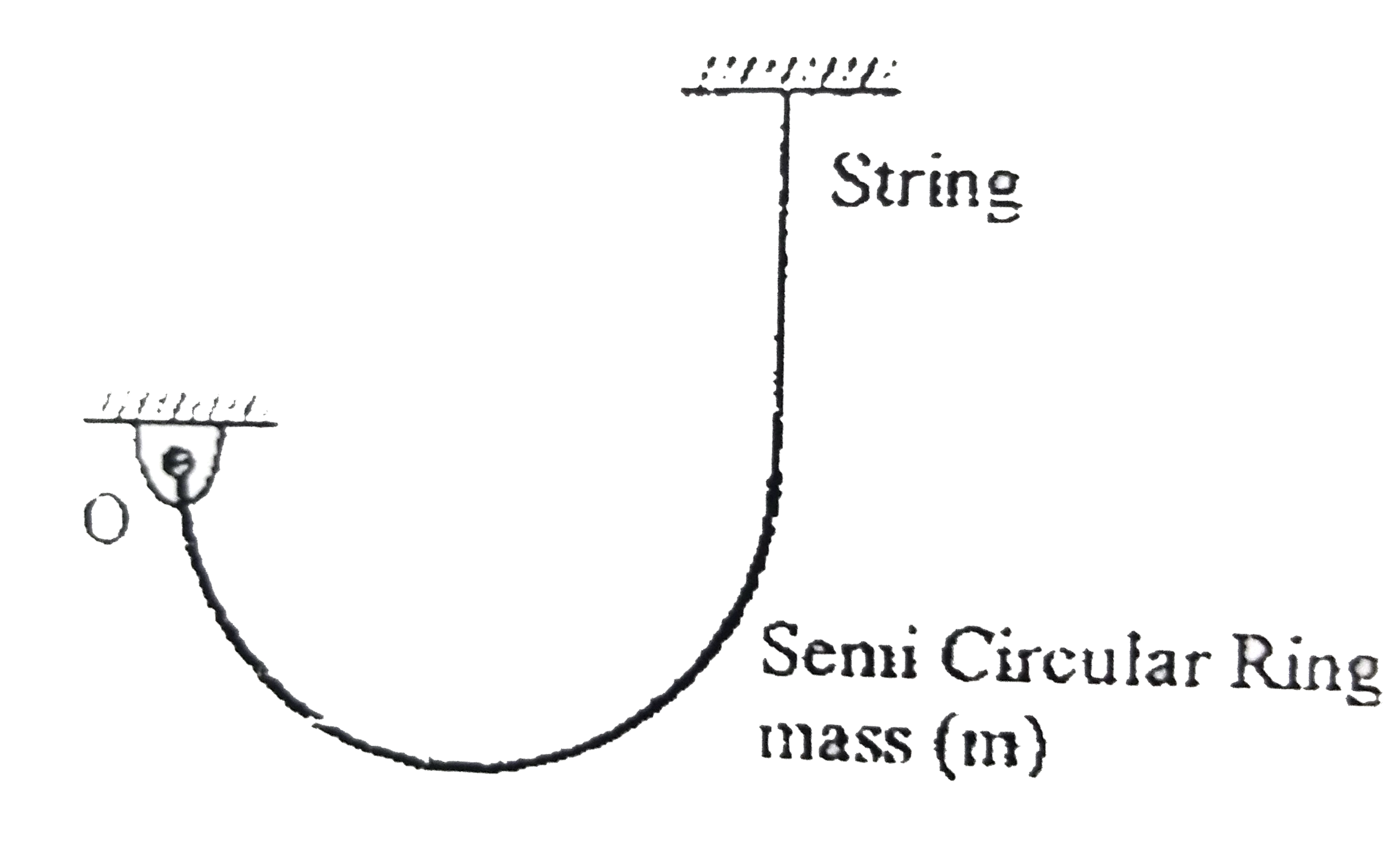 ATension in the string is mg2BAngular acceleration of the semi circular ring just after we cut the string is g4RCForce due to hinge on the semi circular ring always has non zero vetical componentDAcceleration of centre of mass of the semi circular ring, just after we cut the string, must have horizontal & vertical non zero components.
ATension in the string is mg2BAngular acceleration of the semi circular ring just after we cut the string is g4RCForce due to hinge on the semi circular ring always has non zero vetical componentDAcceleration of centre of mass of the semi circular ring, just after we cut the string, must have horizontal & vertical non zero components.A circular rope of weight W and radius r=R2 is resting on a smooth sphere of radius R The tension in rope is
 AW/(π√6)BW/(π√12)CW/(π√10)Dnone of these
AW/(π√6)BW/(π√12)CW/(π√10)Dnone of theseTwo blocks A and B of equal mass m are connected through a massless string and arranged as shown in the figure. Friction is absent everywhere. When the system is released from rest
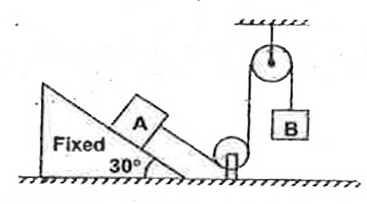 Atension in the string is mg2Btension in the string is mg4Cacceleration of A is g2Dacceleration of A is 3g4
Atension in the string is mg2Btension in the string is mg4Cacceleration of A is g2Dacceleration of A is 3g4
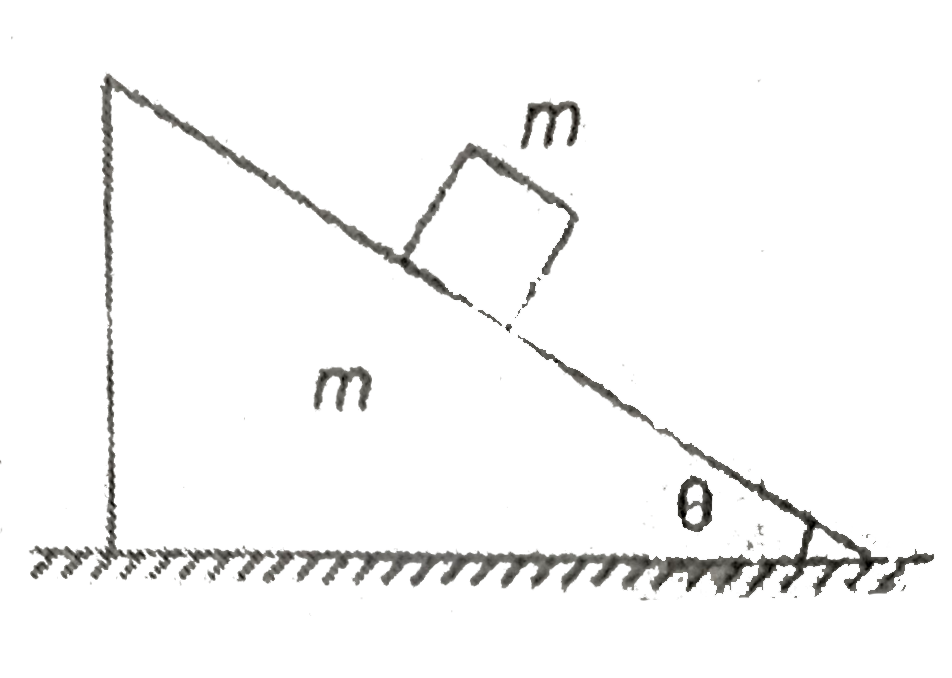
A block of mass m slides down on inclined wedge of same mass m as shown in figure . Friction is absent everywhere . Acceleration of centre of mass of the block and wedge is
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is

View SolutionCalculate the angular frequency of the system shown in figure. Friction is absent everywhere and the threads, spring and pulleys are massless. Given that mA=mB=m.

View SolutionA thin circular ring of mass per unit length p and radius r is rotating at an angular speed ω as shown in figure. The tension in the ring is

View Solution


