A uniform horizontal beam of length L and mass M is attached to a wall by a pin connection. Its far end is supported by a cable that makes an angle θ with the horizontal . If a man of mass 'm' stands at a distance l from the wall , find the tension in the cable in equilibrium.
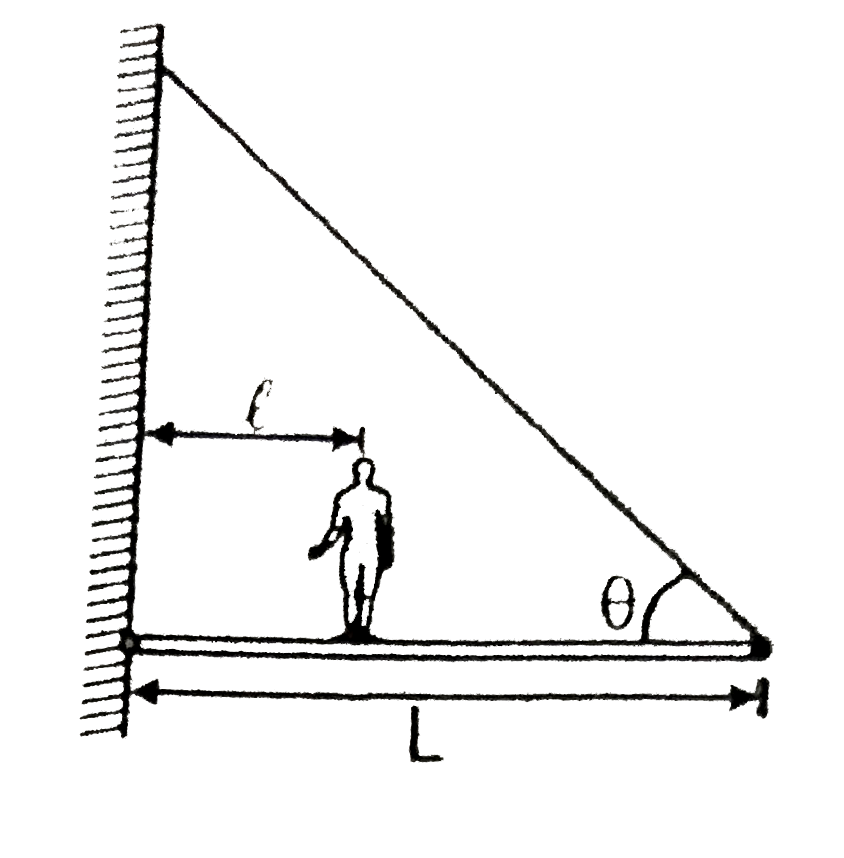
The correct Answer is:T=2mgl+MgL2Lsinθ
For rotational equilibrium
Taking torues about A
( so that torque due hinge force on the rod about A=0)
mg.l+Mg.L2=Tsinθ.L
⇒T=2mgl+MgL2Lsinθ.....Ans.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 605videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp616videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 589videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.
View SolutionIn figure a thin horizontal bar AB of negligible weight and length L is pinned to a vertical wall at A and supported at B by a thin wire BC that makes an angle θ with the horizontal. A weight W can be moved anywhere along the bar; its position is defined by the distance x from the wall of its centre of mass. As a function of x, the horizontal component of the reaction at the hinge A is?
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod is rested on a wall and its lower end is tied wall with the help of a horizontal string of negligble mass as shown. Length of rod is Land height of the wall is h. What will be tension in the string ?
 Amglsinθ2hcosθBmglcos2θ2hsinθCmglsinθcos2θ2hDmgl2hsinθcos2θ
Amglsinθ2hcosθBmglcos2θ2hsinθCmglsinθcos2θ2hDmgl2hsinθcos2θ - Question 2 - Select One
A uniform rod of length 3L and mass m is suspended from a horizontal roof by two strings of length L and 2L as shown. Then the tension in the left string of length L is :
 AmgBmg4Cmg2Dmg3
AmgBmg4Cmg2Dmg3 - Question 3 - Select One
A simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle θ with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
At=2π√l/gBt=2π√lcosθ/gCT=4π2mlt2DThe bob is in equilibrium
A ring of mass M is rolling down an inclined plane . The length of this plane is L . It makes an angle θ with the horizontal . Find the velocity of the centre of mass of the ring at the centre of the plane.
View SolutionIf a simple pendulum of mass m is released from a horizontal position, find the tension in the string as a function of the angle θ with the horizontal.
View SolutionA uniform rod of mass m and length L is suspended through two vertical strings of equal lengths fixed at ends. A small object of mass 2m is placed at distance L/4 from the left end. Find the tensions in the two strings.
View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
View SolutionA uniform stick of mass M is placed in a frictionless well as shown. The stick makes an angle θ with the horizontal. Then the force which the vertical wall exerts on right end of stick is :
 View Solution
View Solution

